Brute force Study

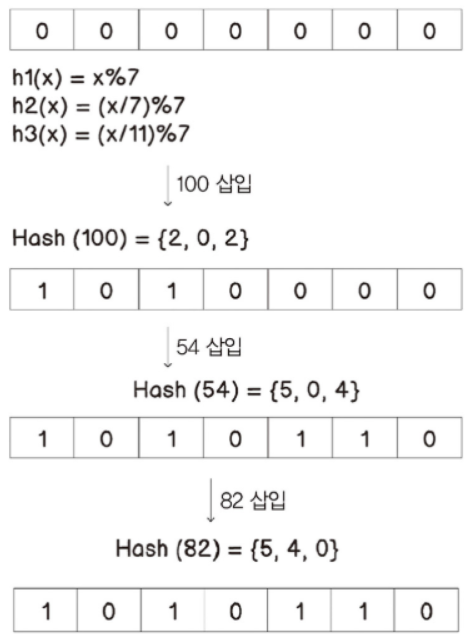
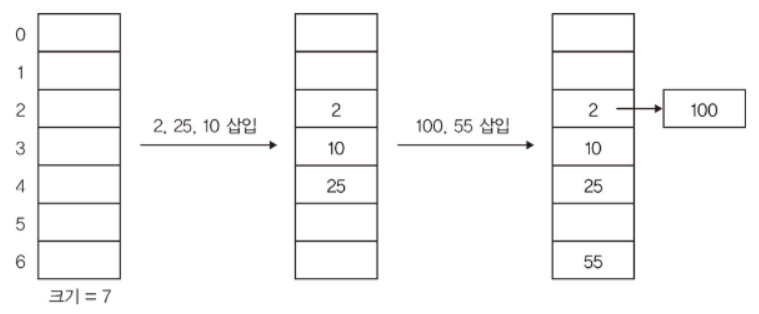
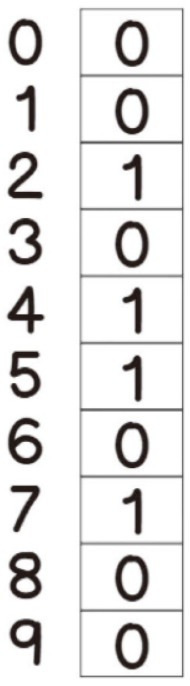
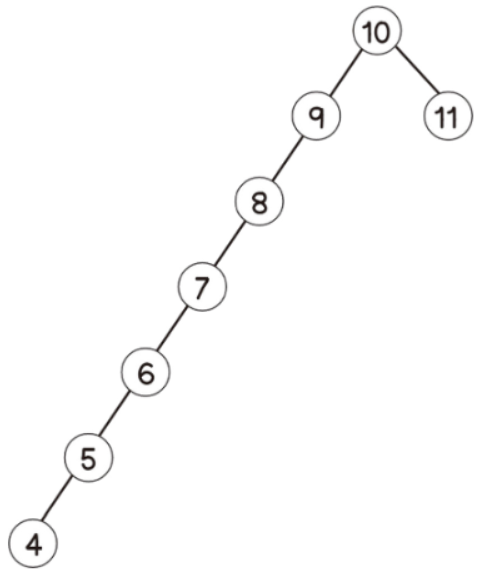
블룸 필터(bloom filter)블룸 필터는 해시 테이블에 비해 공간 효율이 매우 높은 방법이지만, 결정적(deterministic) 솔루션 대신 부정확한 결과를 얻을 수 있다.거짓-부정(false-negative)dl 이 없다는 것은 보장하지만, 거짓-긍정(false-positive)는 나올 수 있다.즉, 특정 원소가 존재한다는 긍정적인 답변을 받을 경우, 이 원소는 실제로 있을 수도 있고 없을 수도 있다.그러나 특정 원소가 존재하지 않는다는 부정적인 답변을 받았다면 이 원소는 확실히 없다뻐꾸기 해싱과 마찬가지로 블룸 필터도 여러 개의 해시 함수를 사용한다정확도를 위해 세 개 이상을 사용해야 한다블룸 필터는 실제 값을 저장하지는 않으며, 대신 특정 값이 있는지 없는지를 나타내는 부울 타입 배열을 사용..

해시 테이블에서 충돌다수의 키를 저장할 수 없는 문제를 해결해보자체이닝앞에서는 하나의 해시 값에 대해 하나의 원소만을 저장했다.따라서 특정 해시 값 위치에 이미 원소가 존재한다면 새로운 값과 예전 값 중 하나를 버릴 수밖에 없었다.체이닝(chaining)은 두 값을 모두 저장할 수 있는 여러 방법 중 하나이다이 방법은 해시 테이블의 특정 위치에서 하나의 키를 저장하는 것이 아니라, 하나의 연결 리스트를 저장한다새로 삽입된 키에 의해 충돌이 발생하면, 리스트의 맨 뒤에 새로운 키를 추가한다따라서 다수의 원소를 원하는 만큼 저장할 수 있다벡터 대신 연결 리스트를 사용하는 이유는, 특정 위치의 원소를 빠르게 삭제하기 위함이다Example) 체이닝을 사용하는 해시 테이블#include #include #incl..

해시 테이블lookup(룩업, 조회)는 특정 원소가 컨테이너에 있는지 확인하거나 또는 컨테이너에서 특정 키(key)에 해당하는 값(value)를 찾는 작업을 의미한다DB에서 원하는 자료를 찾거나, 사전에서 단어의 뜻을 찾는 문제들이 이에 해당모든 원소를 선형으로 검토하여 원하는 값을 찾는 작업은 일반적으로 매우 많은 시간이 소요된다O(N) 시간 복잡도를 가짐이 작업을 훨씬 빠르게 수행할 수 있는 효과적인 알고리즘이 필요하다.해시 테이블과 블룸 필터라는 효과적인 구조에 대해 살펴본다.해시 테이블O(N)을 갖는 선형 검색보다 더 나은 검색 방법은 BST와 같은 속성을 갖도록 높이 균형 트리에 데이터를 저장하는 것이다.시간 복잡도가 O(log N)이므로 선형 검색보다 훨씬 빨라진다검색 횟수가 증가하면 이 정도..

다양한 트리 구조(균형 트리, N-항 트리)균형 트리(Balanced Tree)만약 BST에 다음과 같은 순서로 삽입한다고 생각해보자bst tree;tree.insert(10);tree.insert(9);tree.insert(11);tree.insert(8);tree.insert(7);tree.insert(6);tree.insert(5);tree.insert(4); 다음과 같은 구조를 갖는다전체 트리가 왼쪽으로 편향되어 있다이 경우 검색을 한다면 비교 횟수가 원소 개수와 거의 같아진다만약 다음과 같은 순서로 삽입하여 구성된 트리에서 검색을 한다면bst tree;tree.insert(7);tree.insert(5);tree.insert(9);tree.insert(4);tree.insert(6);tree.i..

다양한 트리 구조(BST)평범한 이진 트리의 효용성은 그리 높지 않음BST, Balanced Tree 등에 대해 알아보자이진 검색 트리(BST, Binary Search Tree)널리 사용되는 형태의 이진 트리다음과 같은 속성이 있다.부모 노드의 값 >= 왼쪽 자식 노드의 값부모 노드의 값 즉, (왼쪽 노드 부모 노드보다 작거나 같은 모든 원소는 항상 왼쪽에 있다.부모 노드보다 크거나 같은 원소는 항상 오른쪽에 있다.완전 이진 트리(complete binary tree)이진트리에서 마지막 레벨을 제외한 모든 노드에 두개의 자식 노드가 있는 트리를 말함이 때 트리의 높이는 log_2(N)이 됨BST에서 원소 검색BST의 속성 때문에 원소 검색을 위해 루트 노드부터 차례대로 값을 비교하는 경우, 각 단계마다..

비선형 문제선형 자료 구조로 표현할 수 없는 대표적인 문제계층적 문제(hierachical problem)순환 종속성 문제(cyclic dependency)계층적 문제ex)회사 조직과 같은 조직 구성은 계층적으로 표현되지만, 선형 자료구조로 표현하기 어렵다선 이수 체계를 갖는 대학교 과정에 대한 종속 관계를 표현할 때에도 마찬가지다.트리를 이용하여 해결순환 종속성ex)SNS에서 사람들과의 친구관계 (그래프)도시와 도시를 잇는 도로망그래프를 이용하여 해결

분리 집합(Disjoint Set)집합의 정의 : 특정 조건에 맞는 원소의 모임분리 집합(Disjoint Set) : 서로 공통된 원소를 갖지 않는, 즉 교집합을 갖지 않는 복수의 집합분리 집합의 개념은 2개 이상의 집합을 일컬을 때만 사용할 수 있음분리 집합은 교집합을 허락하지 않기 때문에 소속 관계가 분명해야 하는 데이터를 다룰 때 아주 유용함ex) 도서 판매 관리 프로그램에서 일반 도서 집합과 베스트셀러 집합을 만들고, 베스트셀러들의 BookPrice가 베스트셀러 집합의 원소가 되도록 함이처럼 분리 집합은 원소 또는 개체가 '어느 집합에 소속되어 있는가?'라는 정보를 바탕으로 무언가를 하는 알고리즘에 응용할 수 있음분리 집합 표현 보통의 트리와 이진 트리는 부모가 자식을 가리키는 포인터를 갖고 있음..

수식 트리(Expression Tree)수식 이진 트리(Expression Binary Tree)라고 부르기도 함일반적으로 다음 두가지 규칙을 가짐피연산자는 잎 노드이다.연산자는 뿌리 노드 또는 가지 노드이다.ex) 1 * 2 + (7 - 8)의 경우 피연산자 1, 2, 7, 8은 모두 잎 노드, 연산자들은 모두 뿌리 노드 or 가지 노드임뿌리 노드와 가지 노드 모두 피연산자를 양쪽 자식으로 가짐여기서 피연산자는 수(Number)일 수도, 또 다른 식(Expressioin)일 수도 있음ex) + 연산자는 하위 트리가 표현하는 수식 (1 * 2)와 (7 - 8)을 피연산자로 가지고 있음수식 트리는 가장 아래에 있는 하위 수식 트리(잎 노드)로 부터 수 또는 계산 결과값을 병합해 올라가는 과정을 반복하며 계..

이진 트리(Binary Tree)하나의 노드가 자식 노드를 2개까지만 가질 수 있는 트리예시수식을 트리 형태로 표현하는 계산하는 수식 이진 트리(Expression Binary Tree)아주 빠른 데이터 검색을 가능하게 하는 이진 탐색 트리(Binary Search Tree)이진 트리의 종류노드의 최대 차수가 2임모든 이진 트리의 자식 노드 수는 0, 1, 2 중 하나포화 이진 트리(Full Binary Tree): 잎 노드를 제외한 모든 노드가 자식을 둘 씩 가진 이진트리잎 노드들이 모두 같은 깊이에 위치한다는 특징을 가짐완전 이진 트리(Complete Binary Tree): 잎 노드들이 트리 왼쪽부터 차곡차곡 채워져 있는 트리포화 이진 트리로 진화하기 전 단계임트리의 노드를 가능한 완전한 모습으로 ..

트리 ADT트리(Tree)란?나무를 닮은 자료구조HTML이나 XML 문서를 다룰 때 사용하는 DOM, 운영체의 파일 시스템 등이 트리 구조로 이루어져 있음트리의 구성요소트리는 뿌리, 가지, 잎 세 가지 요소로 이루어져 있다.세 가지 요소 모두 똑같은 노드이지만 어디에 위치하는지에 따라 불리는 이름이 달라진다뿌리 : 트리 자료구조의 가장 위에 있는 노드를 가리킴가지 : 뿌리와 잎 사이에 있는 모든 노드를 말함잎 노드(단말 노드) : 가지의 끝에 있는 마지막 노드를 잎 노드(단말 노드)라고 한다.부모, 자식 형제 관계가 존재한다. 위 그림을 봐보자노드 B, C, D를 보면 B에서 C와 D가 뻗어 나오는데 이때 B는 C와 D의 부모(Parent)이고, C와 D는 B의 자식(Children)이다.그리고 한 부모..