Brute force Study

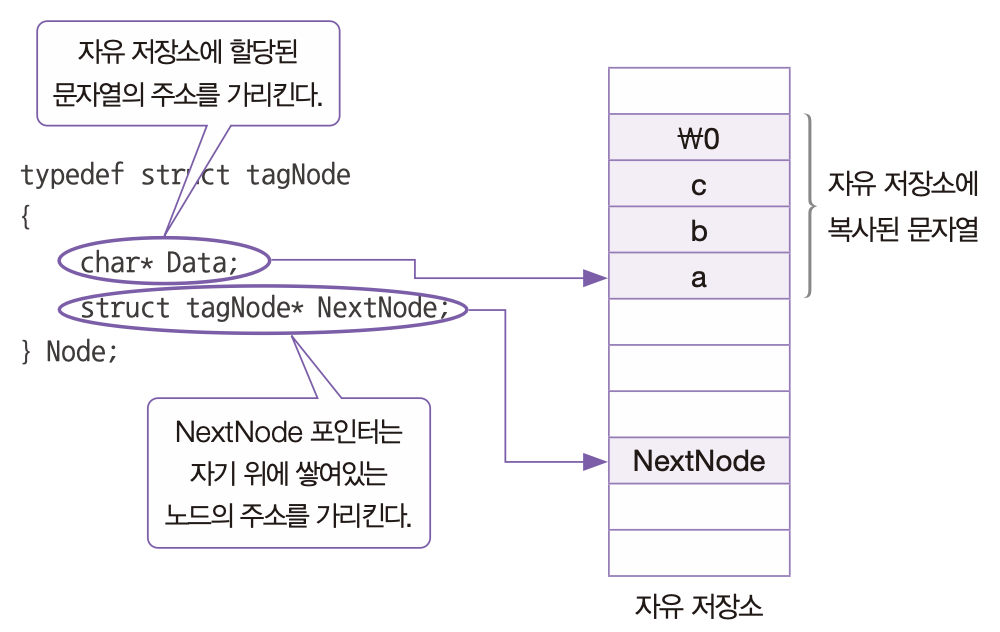
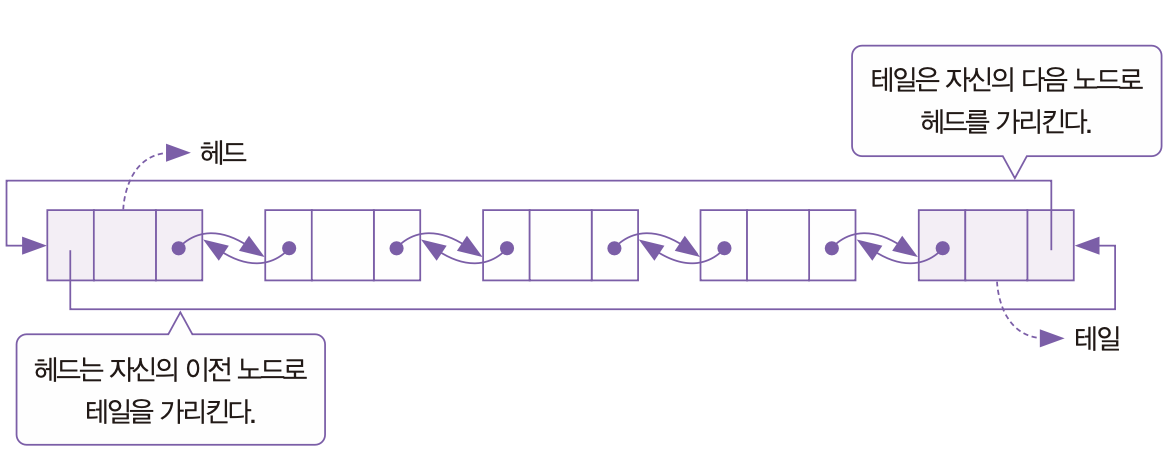
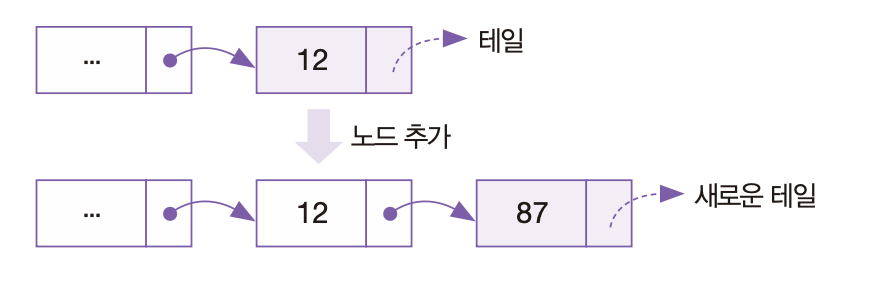
덱(Dequeue) 덱이란? Dequeue : Double-ended Queue 여기선 큐의 출력을 의미하는 Dequeue와 다른 의미로 사용됨 a.k.a 데크 전단, 후단 양쪽에서 push, pop이 가능함 스택과 큐의 장점을 모아둔 자료구조 덱의 종류 스크롤 : 입력이 한쪽 끝으로만 가능하도록 제한, 입력 제한 덱이라고도 함 셀프(Shelf) : 출력이 한쪽 끝으로만 가능하도록 제한, 출력 제한 덱이라고도 함 보통 양쪽에서 입력/출력을 모두 하는 경우는 거의 없어 스크롤이나 셀프를 사용한다 덱의 용도 스케줄링 우선순위 조절 덱의 동작 입력과 출력이 양방향에서 가능하고, 입력과 출력의 순서를 맘대로 정할 수 있음 추가 및 삭제의 실행속도는 O(1) 이중 연결 리스트로 덱 구현 #include #incl..

링크드 큐(Linked Queue) 링크드 리스트를 이용하여 큐를 구현 노드 멤버의 포인터를 이용하여 삽입 / 제거 연산이 이루어짐 삽입을 할 때는 삽입하려는 노드에 후단을 연결 제거를 할 때는 전단 바로 다음 노드에 전단에 대한 포인터를 거두기만 하면 됨 원형 큐(순환 큐)와 다른 점은 용량 제한이 없다는 것이다.(가득 찼는지 확인할 필요 X) 링크드 큐의 기본 연산 보다 직관적으로 설계 및 구현이 가능함 링크드 큐와 노드의 선언 노드의 경우 데이터 필드와 다음 노드에 대한 포인터를 담는다 링크드 큐 구조체의 경우 전단, 후단, 노드 개수를 담는다 // 노드 구조체 typedef struct _Node { char* data; // 노드에 담을 데이터 struct _Node* nextNode; // 다..

큐(Queue)큐의 ADT큐의 개념입력과 출력 창구가 따로 존재하고, 제일 먼저 들어간 데이터가 제일 먼저 나옴(FIFO)큐의 핵심 기능 : 삽입과 제거전단 : 큐의 가장 앞 요소, 제거 연산이 일어나는 곳후단 : 큐의 가장 마지막 요소, 삽입 연산이 일어나는 곳순환 큐(원형 큐)큐를 배열로 구현하는 경우 전단을 제거한 후 요소를 이동하는데 비용이 매우 큼큐의 전단과 후단을 가리키는 변수를 도입삽입과 제거를 거치다 보면 큐의 용량이 줄어듬순환 큐 : 배열의 끝과 시작을 연결함배열의 마지막 요소가 후단인 경우 삽입 연산을 진행하면 배열의 첫 번째 요소가 후단이 된다전단의 경우도 마찬가지삽입이 이루어질 때 후단이 전단을 만나면 큐는 가득 찬 상태가 된다전단과 후단이 만나있는 경우, 공백 상태화 포화 상태를 ..

연결(링크드) 리스트 기반 스택노드의 경우 Data의 주소를 가리키는 참조형과, 자기 위에 쌓여 있는 노드의 주소를 가리키는 NextNode로 구성스택의 용량이나 최상위 노드의 인덱스가 스택의 멤버로 존재하지 않음링크드 리스트의 헤드와 테일에 대한 포인터는 필요함  typedef struct tagNode {char* Data;struct tagNode* NextNode;} Node;typedef struct tagLinkedListStack { Node* List; // 자유 저장소에 존재하는 헤드 노드의 주소를 가리킴 Node* Top; // 자유 저장소에 존재하는 테일 노드의 주소를 가리킴} LinkedListStack;* Top 포인터는 스택의 입출력이 이루어지는 최상위 노드에 대한 포..

배열 기반 스택배열 기반 스택데이터만 담는 구조체로 노드를 표현스택 구조체의 경우 용량, 최상위 노드의 위치, 노드 배열 총 3가지 필드를 가지고 있어야 함typedef struct tagArrayStack { int Capacity; int Top; Node* Nodes; // 자유 저장소에 할당된 배열을 가리키는 용도로 사용(첫 번째 요소)} ArrayStack;배열 기반 스택의 함수생성void AS_CreateStack(ArrayStack** Stack, int Capacity){ // 스택을 자유저장소에 생성 (*Stack) = (ArrayStack*)malloc(sizeof(ArrayStack)); // 입력된 Capacity만큼의 노드를 ..

환형 링크드 리스트(Circular Linked List)a.k.a 원형 연결 리스트싱글 링크드 리스트나 더블 링크드 리스트와 노드 구성은 동일하지만, 헤드와 테일이 연결되어 있음테일의 nextNode는 헤드를 가리키고, 헤드의 prevNode는 테일을 가리킴리스트의 시작과 끝을 미리 알 수 있다 (시작을 알면 끝을 알 수 있고, 끝을 알면 시작을 알 수 있다)DLL의 삽입 함수와 같은 부분의 성능을 많이 개선할 수 있다. (테일에 접근하는 비용이 거의 없으므로)노드를 뒤에서 역순으로 찾아나갈 수 있는 탐색도 구현할 수 있다.환형 더블 링크드 리스트의 주요 연산추가 / 삭제 연산 이외 함수들은 링크드 리스트와 더블 링크드 리스트 함수와 동일함노드 추가 연산비어있는 리스트에 새 노드를 추가하면 이 노드는 ..

이중 연결 리스트(Doubly Linked List)링크드 리스트의 탐색 기능을 개선한 자료구조양방향 탐색이 가능함 (vs 싱글의 단방향)자신 앞에 있는 노드를 가리키는 포인터를 가짐으로써 양방향 탐색이 가능함구조체typedef int ElementType;typedef struct tagNode{ ElementType data; // 저장할 데이터 struct tagNode* prevNode; // 앞 노드의 주소와 데이터 struct tagNode* nextNode; // 뒤 노드의 주소와 데이터} Node; 더블 링크드 리스트의 주요 연산기존 링크드 리스트의 연산과 동일(명세는 구현방식과 상관없이 동일함)노드의 생성/소멸 연산노드의 생성Node* ..

Singly Linked List(SLL) 구현구조체typedef int ElementType; // 필요할 때 원하는 타입으로 바꿔 쓰자typedef struct tagNode { ElementType Data; // 데이터 struct tagNode* NextNode; // 다음 노드} Node;연결 리스트의 주요 연산노드 생성 / 소멸힙(자유 저장소)에 새로운 노드를 생성Node* SLL_CreateNode(ElementType newData) { Node* NewNode = (Node*)malloc(sizeof(Node)); // 새로운 노드 동적할당으로 생성 NewNdoe->Data = newData; // 데이터 저장 NewNode->NextNode = NULL; /..

스택(Stack)의 응용 - 미로 탐색 미로 탐색 문제 미로에 갇힌 주인공이 출구를 찾는 문제 미로가 서로 연결된 여러 개의 방 또는 칸으로 구성되어 있다고 가정 출구를 찾는 과정 기본적인 방법은 시행착오 방법으로서 하나의 경로를 선택하여 한 번 시도해보고 안되면 다시 다른 경로를 시도 이 때, 현재의 경로가 안 될 경우에 다른 경로를 선택해야 하므로 다른 경로들이 어딘가에 저장되어 있어야 함 현재 위치에서 가능한 경로 중에서 가장 가까운 경로를 저장해야 유리함 가장 최근에 저장한 경로가 쉽게 추출되도록 스택을 사용 현재 위치에서 갈 수 있는 방들의 좌표를 스택에 저장한 후 막다른 길을 만나면 아직 가보지 않은 방 중에서 가장 가까운 방으로 다시 돌아가서 새로운 경로를 찾는다 한 번 지니간 방을 다시 가..

스택(Stack)의 응용 - 후위 표기 수식의 계산 수식 수식은 연산자와 피연산자, 괄호로 이루어져 있음. 연산자들은 우선순위가 있어 우선순위가 높은 연산자가 먼저 계산된다. 컴퓨터는 스택을 이용하여 수식을 계산한다. 중위 / 후위 / 전위 표기 수식 중위 표기 수식 사람들이 일반적으로 수식을 표기하는 방식 연산자가 피연산자 사이에 있으면 중위 표기 수식 후위 표기 수식 연산자가 피연산자 뒤에 있으면 후위 표기 수식 전위 표기 수식 연산자가 피연산자 앞에 있으면 전위 표기 수식 예시 2 + 3 * 4 (중위) 234*+ // 후위 표기 수식 +2*34 // 전위 표기 수식 a * b + 5 (중위) ab*5+ // 후위 표기 수식 +*ab5 // 전위 표기 수식 (1 + 2) * 7 (중위) 12+7* ..