이진 트리(Binary Tree)
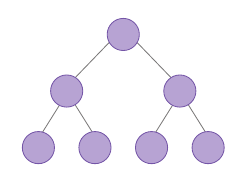
- 하나의 노드가 자식 노드를 2개까지만 가질 수 있는 트리
- 예시
- 수식을 트리 형태로 표현하는 계산하는 수식 이진 트리(Expression Binary Tree)
- 아주 빠른 데이터 검색을 가능하게 하는 이진 탐색 트리(Binary Search Tree)
- 수식을 트리 형태로 표현하는 계산하는 수식 이진 트리(Expression Binary Tree)
이진 트리의 종류
- 노드의 최대 차수가 2임
- 모든 이진 트리의 자식 노드 수는 0, 1, 2 중 하나
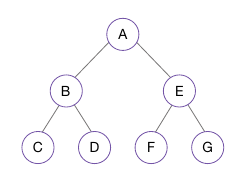
- 포화 이진 트리(Full Binary Tree): 잎 노드를 제외한 모든 노드가 자식을 둘 씩 가진 이진트리
- 잎 노드들이 모두 같은 깊이에 위치한다는 특징을 가짐
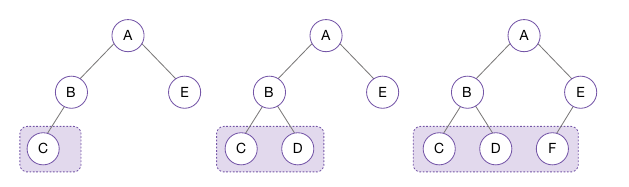
- 완전 이진 트리(Complete Binary Tree): 잎 노드들이 트리 왼쪽부터 차곡차곡 채워져 있는 트리
- 포화 이진 트리로 진화하기 전 단계임
- 트리의 노드를 가능한 완전한 모습으로 유지해야 높은 성능을 낼 수 있기 때문에, 완전한 트리의 모습을 알아야 한다
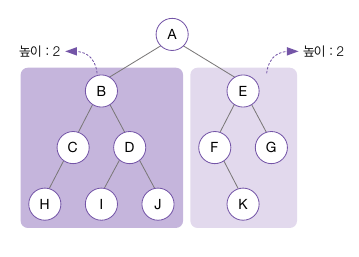
- 높이 균형 트리(Height Balanced Tree): 뿌리 노드를 기준으로 왼쪽 하위 트리와 오른쪽 하위 트리의 높이가 2 이상 차이 나지 않는 이진 트리
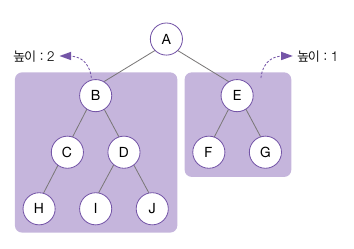
- 완전 높이 균형 트리(Completely Height Balanced Tree): 왼쪽 하위 트리와 오른쪽 하위 트리의 높이가 같은 이진 트리
이진 트리의 순회
- 순회 : 트리 안에서 노드 사이를 이동하는 연산
- 전위 순회(Preorder Traversal) : 뿌리 노드부터 잎 노드까지 아래 방향으로 방문
- 중위 순회(Inorder Traversal) : 왼쪽 하위 트리부터 오른쪽 하위 트리 방향으로 방문
- 후위 순회(Postorder Traversal) : 왼쪽 하위 트리-오른쪽 하위 트리 뿌리 순으로 방문
전위 순회
현재 노드를 방문하고, 그 다음 현재 노드의 왼쪽 하위 노드를, 마지막으로 현재 노드의 오른쪽 하위 노드를 재귀적으로 방문
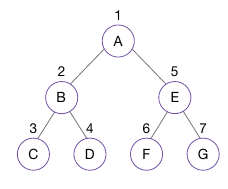
- (1) 뿌리 노드부터 시작하여 아래로 내려오면서 (2) 왼쪽 하위 트리를 방문하고, 방문이 끝나면 (3) 오른쪽 하위 트리를 방문 (/_)
- 위 예시에선 A -> B -> C -> D -> E -> F -> G
- 왼쪽 하위 트리의 뿌리 노드는 B이고, BCD 트리의 왼쪽 하위 트리는 C, 오른쪽 하위 트리는 D이므로, B -> C -> D 순서임
- 전위 순회를 이용하면 이진 트리를 중첩된 괄호로 표현할 수 있음
- (A(B(C, D)), (E(F, G)))
중위 순회
왼쪽 노드를 먼저 방문하고, 그 다음에는 현재 노드, 마지막으로 오른쪽 노드를 방문
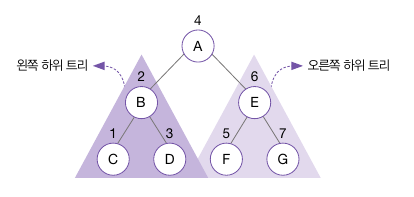
- (1) 왼쪽 하위 트리부터 시작해서 (2) 뿌리를 거쳐 (3) 오른쪽 하위 트리를 방문하는 방법 (/\ )
- 하위 트리 역시 또 다른 하위 트리의 집합이라고 볼 수 있기 때문에, 하위 트리부터 방문
- 하위 트리가 또 다른 하위 트리로 분기할 수 없을 때 까지, 즉 하위 트리가 잎 노드밖에 없을 때 까지 하위 트리들이 계속 이어지는 것
- 왼쪽 하위 트리부터 시작한다 == 가장 왼쪽의 '잎 노드'부터 시작한다
- 이후 부모 노드를 방문한 후 자신의 형제 노드를 방문하는 것으로 이어짐
- 최소 단위의 하위 트리 순회가 끝나면 그 위 단계 하위 트리에 대해 순회를 이어감
- 위 예시에선 C -> B -> D -> A -> F -> E -> G
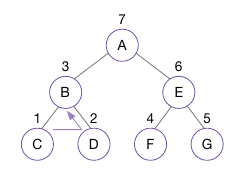
중위 순회가 응용되는 대표 사례 : 수식 트리
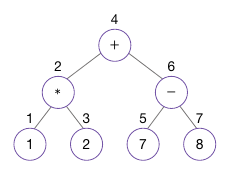
- 수식 트리로 원래의 수식을 찾으려고 한다면 중위 순회를 이용하면 된다
- 노드를 방문할 때 마다 그 노드에 담긴 값을 차례대로 써나간다
- 각 하위 트리의 시작과 끝에는 '(' 와 ')'를 붙여 준다
- 위 예시의 중위 순회 결과 : (1 * 2) + (7 - 8)
후위 순회
두 자식 노드를 먼저 방문한 후, 현재 노드를 방문
- 전위 순회와 반대되는 규칙으로 동작(_\)
- 왼쪽 하위 트리 - 오른쪽 하위 트리 - 뿌리 노드 순으로 방문
- 하위 트리의 하위 트리에 대해서도 똑같이 적용
- 잎 노드를 먼저 방문한다는 특징이 있다
- 위 예시에선 C->D->B -> F->G->E -> A 순으로 방문
- 수식 트리를 후위 순회로 방문하면 후위 표기식이 나오고, 중위 순회로 방문하면 중위 표기식이 나온다
레벨 순회
트리의 맨 위 레벨부터 아래 레벨 까지, 왼쪽 노드에서 오른쪽 노드 순서로 방문한다
- 구현 방법
- 현재 노드에 직접 연결되지 않은 노드로 이동
- 재귀를 사용하지 않고 구현하는 것이 더 쉬움
- 현재 레벨의 노드를 방문할 때 다음 레벨 노드를 미리 큐에 추가하는 방식으로 구현
static void levelOrder(node* start)
{
if(!start)
return;
std::queue<node*> q;
q.push(start);
while(!q.empty())
{
int size = q.size();
for(int i = 0; i < size; i++)
{
auto current = q.front();
q.pop();
std::cout << current->position << ", ";
if(current->first)
q.push(current->first);
if(current->second)
q.push(current->second);
}
std::cout << std::endl;
}
}- 먼저 루트 노드를 방문
- 그 다음에 자식 노드를 방문
- 자식 노드를 방문할 때 해당 노드의 자식 노드를 모두 큐에 추가
- 현재 레벨의 모든 노드 방문이 끝나면 큐에 저장된 노드를 꺼내어 방문
- 큐가 완전히 빌 때 까지 반복하면 레벨 순서 순회가 완료됨
이진 트리의 기본 연산
노드 선언
- 이진 트리 노드를 나타내는 구조체는 다음으로 구성됨
- 왼쪽 자식을 가리키는 Left 필드
- 오른쪽 자식을 가리키는 Right 필드
- 데이터를 담는 Data 필드
typedef struct tagSBTNode {
struct tagSBTNode* Left;
struct tagSBTNode* Right;
ElementType Data;
} SBTNode;노드 생성/소멸 연산
- SBTNode 구조체를 자유 저장소에 생성하는 함수
- malloc() 함수로 SBTNode 구조체의 크기만큼 메모리 공간 할당 후 메모리 공간을 NewNode 포인터에 저장
- NewNode의 Left, Right 필드를 NULL로 초기화, Data 필드에 매개 변수로 입력받은 New Data를 저장
SBTNode* SBT_CreateNode( ElementType NewData ) {
SBTNode* NewNode = (SBTNode*)malloc( sizeof(SBTNode) );
NewNode->Left = NULL;
NewNode->Right = NULL;
NewNode->Data = NewData;
return NewNode;
}- 자유 저장소에서 할당 해제하는 함수
void SBT_DestroyNode( SBTNode* Node ) {
free(Node);
}전위 순회를 응용한 이진 트리 출력
void SBT_PreorderPrintTree( SBTNode* Node ) {
if ( Node == NULL )
return;
// 루트 노드 출력
printf( " %c", Node->Data );
// 왼쪽 하위 트리 출력
SBT_PreorderPrintTree( Node->Left );
// 오른쪽 하위 트리 출력
SBT_PreorderPrintTree( Node->Right );
}중위 순회를 응용한 이진트리 출력
void SBT_InorderPrintTree( SBTNode* Node ) {
if ( Node == NULL )
return;
// 왼쪽 하위 트리 출력
SBT_InorderPrintTree( Node->Left );
// 루트 노드 출력
printf( " %c", Node->Data );
// 오른쪽 하위 트리 출력
SBT_InorderPrintTree( Node->Right );
}후위 순회를 응용한 이진 트리 출력
void SBT_PostorderPrintTree( SBTNode* Node ) {
if ( Node == NULL )
return;
// 왼쪽 하위 트리 출력
SBT_PostorderPrintTree( Node->Left );
// 오른쪽 하위 트리 출력
SBT_PostorderPrintTree( Node->Right );
// 루트 노드 출력
printf( " %c", Node->Data );
}후위 순회를 응용한 트리 소멸
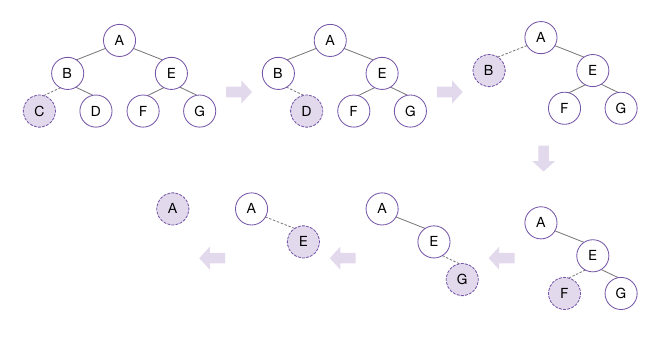
- 트리를 구축할 때 노드들의 생성 순서는 별로 문제되지 않지만, 트리를 파괴할 때는 반드시 잎 노드부터 자유 저장소에서 제거해야 한다
- 잎 노드 부터 방문해 뿌리 노드까지 거슬러 올라가는 후위 순회를 이용하면 이진 트리 전체를 문제 없이 소멸시킬 수 있다.
void SBT_DestroyTree( SBTNode* Node ) {
if ( Node == NULL )
return;
// 왼쪽 하위 트리 소멸
SBT_DestroyTree( Node->Left );
// 오른쪽 하위 트리 소멸
SBT_DestroyTree( Node->Right );
// 루트 노드 소멸
SBT_DestroyNode( Node );
}예제 프로그램
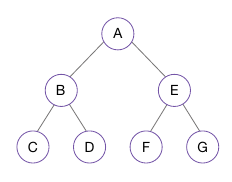
#include "BinaryTree.h"
int main( void ) {
// 노드 생성
SBTNode* A = SBT_CreateNode('A');
SBTNode* B = SBT_CreateNode('B');
SBTNode* C = SBT_CreateNode('C');
SBTNode* D = SBT_CreateNode('D');
SBTNode* E = SBT_CreateNode('E');
SBTNode* F = SBT_CreateNode('F');
SBTNode* G = SBT_CreateNode('G');
// 트리에 노드 추가
A->Left = B;
B->Left = C;
B->Right = D;
A->Right = E;
E->Left = F;
E->Right = G;
// 트리 출력
printf("Preorder ...\n");
SBT_PreorderPrintTree( A );
printf("\n\n");
printf("Inorder ... \n");
SBT_InorderPrintTree( A );
printf("\n\n");
printf("Postorder ... \n");
SBT_PostorderPrintTree( A );
printf("\n");
// 트리 소멸시키기
SBT_DestroyTree( A );
return 0;
}참조) 박상현, 『이것이 자료구조+알고리즘이다 with C언어』, 한빛미디어(2022)
'Computer Science > Data Structure' 카테고리의 다른 글
| [자료구조] 트리 - 분리 집합 (0) | 2024.06.15 |
|---|---|
| [자료구조] 수식 트리 (0) | 2024.06.15 |
| [자료구조] 트리 ADT (0) | 2024.06.15 |
| [자료구조] 덱(Dequeue, 데크) (0) | 2024.03.27 |
| [자료구조] 링크드 큐(Linked Queue) (0) | 2024.03.27 |