트리 ADT
트리(Tree)란?
- 나무를 닮은 자료구조
- HTML이나 XML 문서를 다룰 때 사용하는 DOM, 운영체의 파일 시스템 등이 트리 구조로 이루어져 있음
트리의 구성요소

- 트리는 뿌리, 가지, 잎 세 가지 요소로 이루어져 있다.
- 세 가지 요소 모두 똑같은 노드이지만 어디에 위치하는지에 따라 불리는 이름이 달라진다
- 뿌리 : 트리 자료구조의 가장 위에 있는 노드를 가리킴
- 가지 : 뿌리와 잎 사이에 있는 모든 노드를 말함
- 잎 노드(단말 노드) : 가지의 끝에 있는 마지막 노드를 잎 노드(단말 노드)라고 한다.
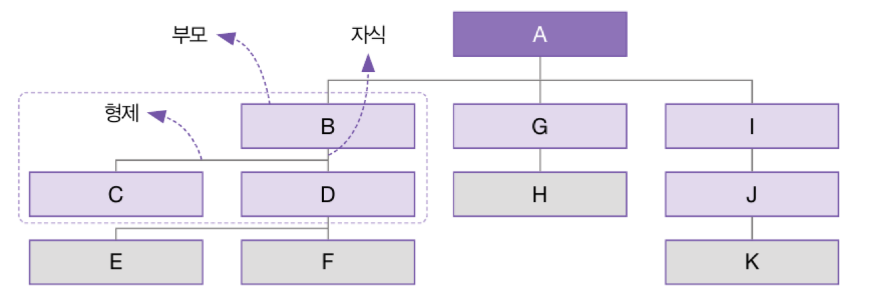
- 부모, 자식 형제 관계가 존재한다. 위 그림을 봐보자
- 노드 B, C, D를 보면 B에서 C와 D가 뻗어 나오는데 이때 B는 C와 D의 부모(Parent)이고, C와 D는 B의 자식(Children)이다.
- 그리고 한 부모 밑에서 태어난 C와 D를 형제(Sibling) 라고 한다.
- 경로 : 한 노드에서 다른 한 노드까지 이르는 길 사이에 있는 노드들의 순서
- 길이(Length) : 출발 노드에서 목적지 노드까지 거쳐야 하는 노드 개수를 말함
- 노드의 깊이(Depth) : 뿌리 노드에서 해당 노드까지 이르는 경로의 길이를 말함
- 레벨(Level) : 깊이가 같은 노드의 집합
- 높이(Height) : 뿌리 노드부터 '가장 깊은 곳'에 있는 잎 노드까지의 길이
- 위 그림에서 가장 깊은 곳에 있는 잎 노드의 깊이가 3이므로 트리의 높이는 3이 됨
- 차수(Degree)
- 노드의 차수 : 그 노드의 자식 노드 개수를 말한다
- 트리의 차수 : 트리 내에 있는 노드들 가운데 자식 노드가 많은 노드를 말한다
트리 표현 방법
- 트리는 다양한 방법으로 표현할 수 있는 ADT
- 트리를 거꾸로 세운 나무 이외에도 여러 방법으로 표현할 수 있음
중첩된 괄호 표현법(Nested Parenthesis)

- 위와 같은 트리를 괄호 표현법으로 표현한다면,
- (A(B(C)(D(E)(F)))(G(H))(I(J(K)))) 로 나타낼 수 있음
- 일기는 다소 어렵지만, 트리를 하나의 공식처럼 표현할 수 있다는 장점을 가지고 있다
중첩된 집합(Nested Set)
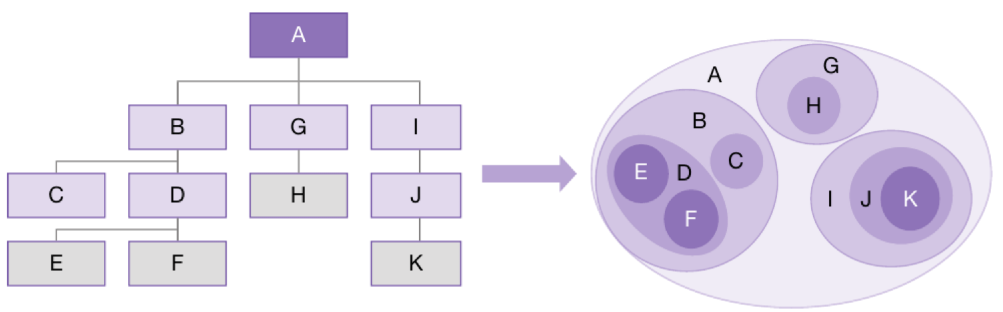
- 트리가 하위 트리의 집합이라는 사실을 이용하여 표현
들여쓰기(Indentation)

- 들여쓰기로 표현한 트리는 자료구조의 계층적인 특징을 잘 나타냄
- ex) 윈도우 탐색기의 폴더 트리
노드 표현 방법
- 노드 표현 방법은 부모와 자식, 형제 노드를 서로 연결 짓는 방법이라고 할 수 있음
- 트리 노드를 표현하는 방법에는 'N-링크'(N-Link) 표현법과 '왼쪽 자식-오른쪽 형제'(Left Child-Right Sibling) 표현법 2가지가 있다.
N-링크(N-Link) 표현법


- N-링크는 노드의 차수가 N이라면 노드가 N개의 링크를 갖고 있는데, 이 링크들이 각각 자식 노드를 가리키도록 노드를 구성하는 방법
- 차수(자식 노드의 수)가 노드마다 달라지는 트리에는 적용하기 힘들다는 단점이 있음
- ex) 폴더 트리의 경우 차수가 0일 수도, 수백 수천일수도 있음.
- 이런 상황에서는 트리 구현이 한층 더 복잡해짐
왼쪽 자식-오른쪽 형제(Left Child-Right Sibling) 표현법

- N-링크 표기법과 달리 위와 같은 문제가 없음
- 왼쪽 자식-오른쪽 형제 표현법은 이름대로 왼쪽 자식과 오른쪽 형제에 대한 포인터만을 갖도록 노드를 구성하는 방법임
- 따라서 N개의 차수를 가진 노드의 표현이 오로지 2개의 포인터(왼쪽 자식 포인터, 오른쪽 형제 포인터)만으로 가능하게 된다.
- 어느 한 노드의 모든 자식 노드를 얻으려면 일단 왼쪽 자식 노드에 대한 포인터만 있으면 됨
- 이 포인터를 통해서 오른쪽 형제 노드의 주소를 얻고, 계속해서 주소를 얻어나가면 모든 자식 노드를 얻을 수 있음
트리의 기본 연산
- 왼쪽 자식-오른쪽 형제 표현법을 사용해서 트리를 활용해보자
노드 선언
- 노드 구조체는 다음으로 구성됨
- 데이터를 담는 Data 필드
- 왼쪽 자식과 오른쪽 형제를 가리키는 2개의 포인터로 구성됨
- 데이터를 담는 Data 필드
typedef char ElementType;
typedef struct tagLCRSNode {
struct tagLCRSNode* LeftChild;
struct tagLCRSNode* RightSibling;
ElementType Data;
} LCRSNode;노드 생성/소멸 연산
- 자유 저장소에 노드를 생성하는 함수
- LCRSNode 구조체에 크기만큼 자유 저장소에 메모리를 할당, 매개 변수 NewData를 Data에 저장한 후 노드의 메모리 주소 반환
LCRSNode* LCRS_CreateNode(ElementType NewData) {
LCRSNode* NewNode = (LCRSNode*)malloc(sizeof(LCRSNode));
NewNode->LeftChild = NULL;
NewNode->RightChild = NULL;
NewNode->Data = NewData;
return NewNode;
}- 노드를 자유 저장소에서 할당 해제하는 함수
void LCRS_DestroyNode( LCRSNode* Node ) {
free(Node);
}자식 노드 연결

- 노드에 자식 노드를 연결하는 함수
- 부모 노드와 이 부모 노드에 연결할 자식 노드를 매개변수로 받음
- 부모 노드인 Parent에게 자식 노드가 있는지 검사
- LeftChild == NULL인지
- 위 경우 Parent의 LeftChild 포인터에 자식 노드 주소를 바로 저장
- LeftChild가 NULL이 아닌 경우 자식 노드가 하나 이상이라는 의미
* RightSibling 포인터를 이용해 가장 오른쪽에 있는 자식 노드를 찾아 그 노드의 RightSibiling에 Child 대입
- LeftChild == NULL인지

void LCRS_AddChildNode(LCRSNode* Parent, LCRSNode *Child) {
if ( Parent->LeftChild == NULL ) {
Parent->LeftChild = Child;
} else {
LCRSNode* TempNode = Parent->LeftChild;
while ( TempNode->RightSibling != NULL )
TempNode = TempNode->RightSibling;
TempNode->RightSibling = Child;
}
}트리 출력
- 완성된 트리를 출력하는 함수
- 트리를 들여쓰기 형식으로 출력
- 제일 앞에 나오는 for 루프가 매개 변수 Depth - 1 만큼 공백을 3칸 출력
- 공백 마지막에는 해당 노드가 누군가의 자식 노드임을 나타내는 '+--'를 덧붙인 후 노드의 데이터를 출력
- 깊이가 0인 뿌리 노드는 제일 앞쪽에 출력되고, 잎 노드는 제일 뒤쪽(깊은 곳)에 출력됨
void LCRS_PrintTree( LCRSNode* Node, int Depth ) {
// 들여쓰기
int i=0;
for ( i=0; i<Depth-1; i++ )
printf(" "); // 공백 3칸
if (Depth > 0) // 자식노드 여부 표시
printf("+--");
// 노드 데이터 출력
printf("%c\n", Node->Data);
if ( Node->LeftChild != NULL )
LCRS_PrintTree(Node->LeftChild, Depth+1);
if ( Node->RightSibling != NULL )
LCRS_PrintTree(Node->RightSibling, Depth);
}예제 프로그램

#include "LCRSTree.h"
int main( void ) {
// 노드 생성
LCRSNode* Root = LCRS_CreateNode('A');
LCRSNode* B = LCRS_CreateNode('B');
LCRSNode* C = LCRS_CreateNode('C');
LCRSNode* D = LCRS_CreateNode('D');
LCRSNode* E = LCRS_CreateNode('E');
LCRSNode* F = LCRS_CreateNode('F');
LCRSNode* G = LCRS_CreateNode('G');
LCRSNode* H = LCRS_CreateNode('H');
LCRSNode* I = LCRS_CreateNode('I');
LCRSNode* J = LCRS_CreateNode('J');
LCRSNode* K = LCRS_CreateNode('K');
// 트리에 노드 추가
LCRS_AddChildNode( Root, B );
LCRS_AddChildNode( B, C );
LCRS_AddChildNode( B, D );
LCRS_AddChildNode( D, E );
LCRS_AddChildNode( D, F );
LCRS_AddChildNode( Root, G );
LCRS_AddChildNode( G, H );
LCRS_AddChildNode( Root, I );
LCRS_AddChildNode( I, J );
LCRS_AddChildNode( J, K );
// 트리 출력
LCRS_PrintTree( Root, 0 );
// 트리 소멸시키기
LCRS_DestroyTree( Root );
return 0;
}참조) 박상현, 『이것이 자료구조+알고리즘이다 with C언어』, 한빛미디어(2022)
'Computer Science > Data Structure' 카테고리의 다른 글
| [자료구조] 수식 트리 (0) | 2024.06.15 |
|---|---|
| [자료구조] 이진 트리 (0) | 2024.06.15 |
| [자료구조] 덱(Dequeue, 데크) (0) | 2024.03.27 |
| [자료구조] 링크드 큐(Linked Queue) (0) | 2024.03.27 |
| [자료구조] 큐와 원형 큐(순환 큐) (0) | 2024.03.27 |