다양한 트리 구조(균형 트리, N-항 트리)
균형 트리(Balanced Tree)
만약 BST에 다음과 같은 순서로 삽입한다고 생각해보자
bst tree;
tree.insert(10);
tree.insert(9);
tree.insert(11);
tree.insert(8);
tree.insert(7);
tree.insert(6);
tree.insert(5);
tree.insert(4);
다음과 같은 구조를 갖는다
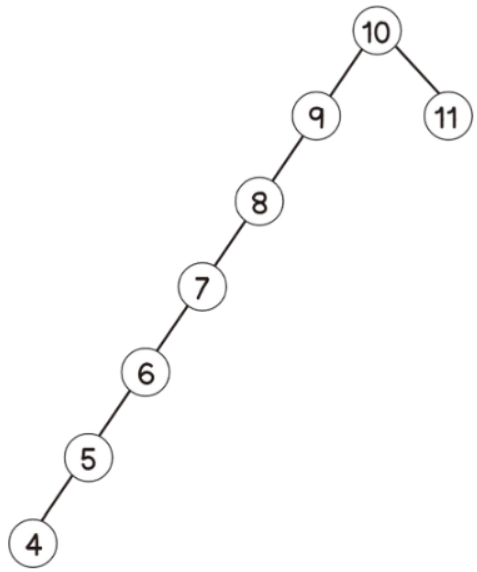
- 전체 트리가 왼쪽으로 편향되어 있다
- 이 경우 검색을 한다면 비교 횟수가 원소 개수와 거의 같아진다
만약 다음과 같은 순서로 삽입하여 구성된 트리에서 검색을 한다면
bst tree;
tree.insert(7);
tree.insert(5);
tree.insert(9);
tree.insert(4);
tree.insert(6);
tree.insert(10);
tree.insert(11);
tree.insert(8);
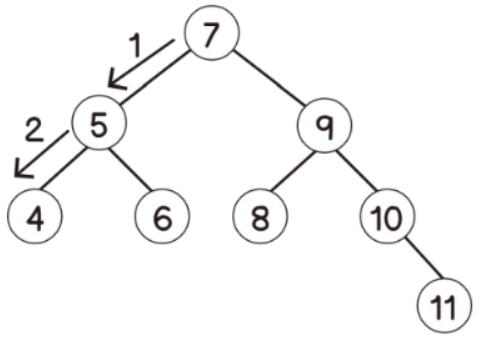
- 단계가 크게 감소한다
- 위와 같은 트리는 편향되지 않은 상태이며, 이러한 트리를 균형이 잡혔다고 한다
- 즉, find() 함수의 시간 복잡도는 단순히 원소의 개수에 영향을 받는게 아니라, 트리의 형태에도 영향을 받는다
- 검색을 하계 되면 항상 트리의 아래쪽으로 한 단계씩 나아가서 리프 노드에서 끝난다
- 따라서 검색에 필요한 단계의 수는 BST의 최대 레벨 수보다는 작다.
- 검색의 시간 복잡도는 O(높이)로 표현할 수 있다
- 원소 검색의 시간 복잡도를 최적화 하려면, 트리의 높이가 최적화 되어야 한다.
- 이러한 작업을 트리의 균형 잡기라고 한다
- 트리의 균형을 잡기 위해서는 원소 삽입/삭제 이후 트리 구성을 조정해야 한다
- 이렇게 조정되어 편향성이 줄어든 이진 검색 트리를 높이-균형 BST(height-balanced BST)라고 한다
- 이를 통해 AVL 트리, 레드-블랙 트리 같은 다양한 트리를 만들 수 있다.
- AVL 트리의 기본 아이디어는 BST 속성을 유지하며 트리의 높이 균형을 잡기 위해 약간의 회전을 수행한다
- 이를 통해 AVL 트리, 레드-블랙 트리 같은 다양한 트리를 만들 수 있다.
N-항 트리(N-ary tree)
- 각 노드가 N개의 자식을 가질 수 있다.
- N개의 자식 노드는 벡터를 이용하여 저장할 수 있다
- 구조체
struct nTree
{
int data;
std::vector<nTree*> children;
};- 각각의 노드는 임의 개수의 자식을 거느릴 수 있다.
- 전체 트리도 임의의 형태를 가지게 됨
- 평범한 N-항 트리는 그다지 유용하지 않아, 요구사항에 맞는 트리를 만들어 사용해야 한다
- 컴퓨터 분야에서 N항 트리를 사용하는 대표적인 예
- 컴퓨터 파일 시스템 구조
- 컴파일러
'Computer Science > Data Structure' 카테고리의 다른 글
| [자료구조] 해시 테이블(2)- 충돌 (0) | 2024.06.23 |
|---|---|
| [자료구조] 해시 테이블(1) (0) | 2024.06.23 |
| [자료구조] 다양한 트리 구조(BST) (0) | 2024.06.18 |
| [자료구조] 비선형 문제 (0) | 2024.06.18 |
| [자료구조] 트리 - 분리 집합 (0) | 2024.06.15 |