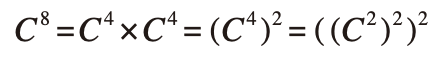Brute force Study

거듭 제곱 계산법C^2을 계산하기 위해서는 다음과 같이 C 자신을 두 번 곱해야 한다C^2 = C X CC^n을 계산하려면 C 자신을 n번 곱해야 한다.이를 코드로 바꾸면 다음과 같다int Power( int Base, int Exponent ){ int i=0; int Result = 1; // C^0은 1이므로 for ( i=0; i 지수 크기만큼 곱셈을 수행하므로 O(n) 수행 시간을 소요한다는 사실을 알 수 있다.이보다 더 빠른 방법은 없을까?접근C^8은 C x C x C x C x C x C x C x C 로 정의되지만다음과 같이 표현할 수도 있다. C^2을 구한 뒤 제곱을 두 번 더 반복하여 결국 세 번의 곱셈만 수행함으로써 같은 결과를 얻을 수 있다.하지만 이 방법을 모든 제곱 연산에 적용할..

분할 정복을 적용하는데 있어서 주의할 점분할 정복이 부적절한 경우입력이 분할될 때 마다 분할된 부분 문제의 입력 크기의 합이 분할되기 전의 입력 크기보다 커지는 경우ex) 피보나치 수 구하기recursive하게 정의 : F(n) = F(n-1) + F(n-2) with F(0) = 0 and F(1) = 1.예를 들어, n 번째의 피보나치 수를 구하는데 F(n) = F(n-1) + F(n-2)로 정의되므로 재귀 호출을 사용하는 것이 자연스러워 보이나, 이 경우의 입력은 1개이지만, 사실상 n의 값 자체가 입력 크기인 것이다따라서 n이라는 숫자로 인해 2개의 부분 문제인 F(n-1)과 F(n-2)가 만들어지고, 2개의 입력 크기의 합이 (n-1) + (n-2) = (2n-3)이 되어서, 분할 후 입력 크기..

트로미노 타일로 체스판 채우기구멍이 하나 있는 정사각형 체스판을 L 자 모양의 트로미노(tromino) 타일로 채울 수 있는가?체스판의 크기를 2^k ×2^k 라 가정  접근가장 작은 크기의 부문제인 “구멍이 하나 있는 2×2 체스판” 에 대해 어느 곳에 구멍이 있더라도 체스판을 채우는 것이 가능한가? -->  “구멍이 하나 있는 2^k×2^k 체스판”에서 “구멍이 하나 있는 (2^1)×(2^1) 체스판”으로 문제를 점차 줄여나갈 수만 있다면 분할정복 알고리즘을 사용하여 해결 가능하다. 아이디어정사각형의 체스판을 4개의 작은 체스판으로 나눈다하나의 2^k X 2^k 체스판 문제에서 4개의 2^(k-1) X 2^(k-1) 체스판 문제로 분할한다.그런데, 3개의 2^(k-1) X 2^(k-1) 체스판에는 구..

최근접 점의 쌍 문제란?2차원 평면상의 n개의 점이 입력으로 주어질 때, 거리가 가장 가까운 한 쌍의 점을 찾는 문제 가장 간단한 해결 방법모든 점에 대하여 각각의 두 점 사이의 거리를 계산하여 가장 가까운점의 쌍을 찾다.nC2 X O(1) = O(n^2)이것보다 효율적인 방법은 없을까?분할 정복을 이용한 해결 방법1. n개의 점을 1/2로 분할하여 각각의 부분 문제에서 최근접 점의 쌍을 찾고, 2개의 부분해 중에서 짧은 거리 (d)를 가진 점의 쌍을 일단 찾는다. (recursive하게 반복하여 구함)2. [결합] 2개의 부분해를 취합할 때에는 반드시 두 부분 문제서 각각 한 점씩 포함되는 점의 쌍 중에서 그 거리가 d 보다 작은 쌍을 찾는다. (중간영역 고려!)만일 이러한 쌍이 있다면 그런 쌍 중에 ..

분할 정복 기법과 C++ 표준 라이브러리 함수앞선 게시글에서 알고리즘에 필요한 기능을 직접 구현해보았지만, C++ 표준 라이브러리는 미리 정의된 다수의 알고리즘 함수를 제공하고 있다.std::binary_search()std::binary_search() 함수는 정렬된 범위에서 특정 값을 찾기 위해 이진 검색 알고리즘을 사용합니다. 이 함수는 주어진 값이 정렬된 범위 내에 존재하는지를 확인하고, 존재 여부에 따라 true 또는 false를 반환합니다.헤더 파일:#include 사용법:bool binary_search(InputIt first, InputIt last, const T& value);bool binary_search(InputIt first, InputIt last, const T& valu..

선택 문제n개의 숫자들 중에서 k 번째로 작은 숫자를 찾는 문제이다.선택 문제 해결 방법간단한 방법 1.  최소 숫자를 k번 찾는다. 단 최소 숫자를 찾은 뒤에는 입력에서 최소 숫자를 제거한다숫자를 제거하는 과정에서 추가 수행시간 또는 추가 메모리가 필요하다O(kn)간단한 방법 2 : 숫자들을 정렬한 후 k 번째 숫자를 찾는다.O(nlogn)의 수행 시간이 필요하다k가 작을 경우 최소 숫자를 k번 찾는 것이 유리하고, 그렇지 않은 경우 정렬하여 찾는 것이 유리하다이진탐색 아이디어를 활용해보자이진 탐색에서는 정렬된 입력의 중간에 있는 숫자와 찾고자 하는 숫자를 비교함으로써 입력을 1/2로 나눈 두 부분 중에서 한 부분만 검색했다.분할 후 각 그룹의 크기를 알아야 k번째 작은 숫자가 어느 그룹에 있는지를 알..

퀵 정렬이란?이전 챕터에서 본 병합 정렬의 목적이 대용량의 데이터를 정렬하는 것이라면, 퀵 정렬은 평균 실행 시간을 줄이는 것이 목표이다.분할 정복 접근법을 이용하는 기본 아이디어는 병합 정렬과 동일하다. 다만 퀵 정렬의 핵심은 병합이 아니라 분할이다.퀵 정렬은 문제를 2개의 부분문제로 분할하는데, 각 부분문제의 크기가 일정하지 않은 형태의 비균등 분할 정복 알고리즘이다퀵 정렬의 분할 연산 방법입력 배열이 주어지고, 입력 배열 중 피벗(pivot) 원소 P를 선택했을 경우, 퀵 정렬을 위한 분할 연산은 다음 두 단계로 이루어진다 입력 배열을 두 개의 부분 배열 L과 R로 나눈다. L은 입력 배열에서 P보다 작거나 같은 원소를 포함하는 부분 배열이고, R은 입력 배열에서 P보다 큰 원소를 포함하는 부분 배..

분할 정복을 이용한 정렬 알고리즘유명한 알고리즘 문제 중의 하나인 정렬(sorting)을 분할 정복으로 구현하는 방법에 대해 알아보자 정렬 알고리즘 구현에 있어 필요한 요구사항모든 데이터 타입에 대해 동작해야 한다. 심지어 C++ 구조체, 클래스에 대해서도 서로 다른 멤버를 기준으로 정렬할 수 있어야 한다많은 양의 데이터를 처리할 수 있어야 한다.점근적 시간 복잡도 측면이나 실제 동작 시에 빠르게 동작한다현실적으로 두 번째와 세 번째 요구사항을 동시에 만족하기는 어렵다. 두 번째 요구사항은 외부 정렬(external sorting), 즉 컴퓨터의 메모리에 데이터가 상주하지 않은 상태에서 수행되는 정렬을 필요로 한다.외부 정렬 알고리즘은 실행 중 임의 시점에서 전체 데이터의 일부만을 메모리에 올려놓고 동작..

이진 검색(binary search) (a.k.a 이진 탐색) 일반적인 검색 문제정렬되어 있는 정수 시퀀스가 있고, 여기에 숫자 N이 있는지 확인하려고 한다.이러한 검색 문제는 두 가지 방법으로 접근할 수 있다.  선형 검색(linear search)시퀀스 전체 원소를 방문하면서 해당 원소가 N과 같은지를 확인하는 방식이다.bool linear_search(int n, vector& sequence) { for (auto i : sequence) { if (i == n) { return true; } } return false;} 장점 : 입력 시퀀스의 정렬 여부와 상관 없이 항상 잘 동작한다단점 : 효율적이지 않음.O(N)주어진 배열이 정렬되..

분할 정복 설계 패러다임효율적인 알고리즘을 설계하기 위한 일반적인 접근 방법이 개발되어 다양한 문제 해결에 사용되고 있다.분할 정복(divide-and-conquer)은 가장 널리 사용되는 알고리즘 설계 패러다임 중 하나이다.분할 정복 알고리즘이란?주어진 문제를 작은 부분 문제로 나누고, 나줘진 각 부분 문제의 솔루션을 구하고, 각 부분 문제 솔루션을 합쳐서 전체 문제에 대한 솔루션을 구하는 방식binary search(이진 탐색), quick sort(퀵 정렬), merge sort(병합 정렬), matrix mulitplication(행렬 곱셈), Fast Fourier Trnasform(고속 푸리에 변환), skyline algorithm(스카이라인 알고리즘) 등에서 사용되는 패러다임이다.분할 정복..