선택 문제
n개의 숫자들 중에서 k 번째로 작은 숫자를 찾는 문제이다.
선택 문제 해결 방법
- 간단한 방법 1. 최소 숫자를 k번 찾는다. 단 최소 숫자를 찾은 뒤에는 입력에서 최소 숫자를 제거한다
- 숫자를 제거하는 과정에서 추가 수행시간 또는 추가 메모리가 필요하다
- O(kn)
- 간단한 방법 2 : 숫자들을 정렬한 후 k 번째 숫자를 찾는다.
- O(nlogn)의 수행 시간이 필요하다
- k가 작을 경우 최소 숫자를 k번 찾는 것이 유리하고, 그렇지 않은 경우 정렬하여 찾는 것이 유리하다
이진탐색 아이디어를 활용해보자
- 이진 탐색에서는 정렬된 입력의 중간에 있는 숫자와 찾고자 하는 숫자를 비교함으로써 입력을 1/2로 나눈 두 부분 중에서 한 부분만 검색했다.
- 분할 후 각 그룹의 크기를 알아야 k번째 작은 숫자가 어느 그룹에 있는지를 알 수 있고, 그 그룹에서 몇 번재로 작은 숫자를 찾아야 하는지를 알 수 있다.
- Small group에 k 번째 작은 숫자가 속하면 k번째 작은 숫자를 small group에서 찾으면 된다.
- Large group에 k 번째 작은 숫자가 있는 경우에는 (k - |Small group| - 1) 번째로 작은 숫자를 Large group에서 찾으면 된다.
- |Small group| : Small group에 있는 숫자의 개수
- 1은 피봇
크게 보면 과정은 다음과 같다.
1. 주어진 입력에서 피봇을 랜덤으로 선택하고, 피봇보다 작은 수는 피봇의 왼쪽으로 옮기고 피봇보다 큰 수는 피봇의 왼쪽으로 옮긴다
2. k가 Small group의 크기보다 작으면 Small group에서 1번 과정을 반복한다.
k가 Small group의 크기보다 크면 large group에서 (k - (위에서 구한Small group의 크기) - 1)번째 수를 찾는다
k == (Small group의 크기) + 1 이면 피봇이 찾고자 하는 수이다.
슈도 코드
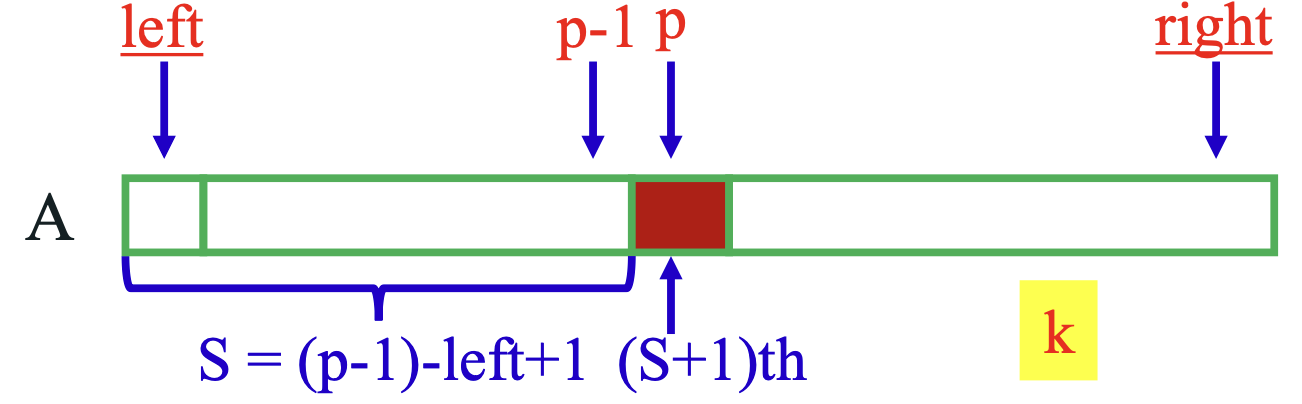
Selection(A, left, right, k)
입력: A[left]~A[right]와 k, 단, 1≤k≤|A|, |A|=right-left+1
출력: A[left]~A[right]에서 k 번째 작은 원소
1. 피봇을 A[left]~A[right]에서 랜덤하게 선택하고,
1) 피봇과 A[left]의 자리를 바꾼 후,
2) 피봇과 배열의 각 원소를 비교하여 피봇보다 작은 숫자는 A[left]~A[p-1]로 옮기고,
3) 피봇보다 큰 숫자는 A[p+1]~A[right]로 옮기며, 피봇은 A[p]에 놓는다.
2. S = (p-1)-left+1 // S = Small group의 크기
3. if ( k ≤ S ) Selection(A, left, p-1, k) // Small group에서 찾기
4. else if ( k = S +1) return A[p] // 피봇 = k번째 작은 숫자
5. else Selection(A, p+1 right, k-S-1) // large group에서 찾기
지금까지 살펴본 분할 정복 알고리즘은 각 단계에서 문제를 정확하게 두 개의 부분 문제로 나눴다. 그러나 각 단계에서 문제를 두 개 이상으로 분할하는 것이 더 유리한 경우도 있다.
시간 복잡도
- Pivot을 정하고 파티션을 나누려고 할 때, pivot 배열 값과 배열 내 모든 값과 비교하여 partition을 나누는 것을 고려해야 한다.
- 최소 숫자를 k번 찾고, 배열 내 모든 값과 비교하므로 O(kn)이다.
- 최선의 경우 시간 복잡도
- 처음 파티션을 위해 피봇을 골랐는데 pivot point가 배열에서 위치(인덱스)가 k인 경우
- n-1번 비교한 후 파티션이 되므로 B(n) = n - 1
- 최악의 경우 시간 복잡도
- 파티션 대상의 크기가 1이 될 때 까지 계속할 경우
- 비교 횟수 = (n-1) + (n-2) + ... + 1 = n(n-1) / 2
- 따라서 W(n) = O(n^2)
- 평균적인 경우 시간 복잡도
- 선택 알고리즘은 피봇을 랜덤하게 정해 피봇에 따라 입력 리스트의 분할이 결정된다
- 피봇이 입력 리스트를 너무 한 쪽으로 치우치게 분할하게 되면 수행시간이 길어진다는 것을 최악의 경우에서 확인했다
- 입력을 한쪽으로 치우치게 분할될 확률은 ½
- 분할된 두 그룹 중의 하나의 크기가 입력 크기의 3/4과 같거나 그 보다 크게 분할하면 나쁜 (bad) 분할이라 하고 아니면 좋은 (good) 분할이라고 하자.

- 입력을 치우치게 분할하지 않을 확률이 ½이므로 평균 두 번의 partition 한 번은 good 분할이다
- 기댓값이 2회
- 매 2회 피봇을 호출마다 good 분할이 되므로, good 분할만 연속하여 이루어졌을 때만의 시간을 구하여 그 값에 2를 곱하면 평균 시간복잡도를 얻을 수 있다
- Good 분할이 반복될 경우, list 크기가 n에서부터 3/4배로 연속적으로 감소되고, 리스트 크기가 1일 때 분할과정이 멈춘다
- A(n)=2[n + 3/4n + (3/4)2n +(3/4)3n +… +(3/4)i-1n +(3/4)in]
- = 2n[1 + 3/4 + (3/4)2 +(3/4)3 +… +(3/4)i-1 +(3/4)i]
- = O(n)
응용
- k 번째 작은 수를 선형 시간에 찾을 수 있게 해준다. 데이터 분석을 위한 중앙값을 찾는데 활용된다
선형 시간 선택 문제
지금까지 살펴본 분할 정복 알고리즘은 각 단계에서 문제를 정혹하게 두 개의 부분 문제로 나눴다. 그러나 문제를 두 개 이상으로 분할하는 것이 더 유리한 경우도 있다. 이러한 문제 중 하나가 선형 시간 선택 문제(linear time selection)이다.
위에서 말한 선택 문제처럼, 정렬되지 않은 원소의 집합 S가 주어졌을 때, 여기서 i번째로 작은 원소를 찾아야 한다. 이 책에서는 다음과 같은 솔루션을 제공한다
- 입력 벡터 V가 주어지면 여기서 i번째로 작은 원소를 찾으려고 한다.
- 입력 벡터 V를 V1, V2, V3.... Vn/5로 분할한다. 각각의 부분 벡터 Vi는 다섯 개의 원소를 가지고 있고, 마지막 Vn/5는 다섯 개 이하의 원소를 가질 수 있다.
- 각각의 Vi를 정렬한다
- 각각의 Vi에서 중앙값 mi를 구하고, 이를 모아서 집합 M을 생성한다
- 집합 M에서 중앙값 q를 찾는다
- q를 피벗으로 삼아 전체 벡터 V를 L과 R의 두 벡터로 분할한다
- 이런한 방식으로 분할하면 부분 벡터 L은 q보다 작은 원소만을 가지고, 부분 벡터 R은 q보다 큰 원소만을 포함하게 된다. 이 때 L에 (k-1) 개의 원소가 있다고 가정해보자.
- i = k이면, q는 V의 i번째 원소이다
- i < k 이면, V = L로 설정하고 맨 위 1단계로 이동한다
- i > k 이면, V = R 로 설정하고 맨 위 1단계로 이동한다
선형 시간 선택 알고리즘 구현
두 반복자 사이의 중간 값을 찾는 함수를 작성
template<typename T>
auto find_median(typename std::vector<T>::iterator begin,
typename std::vector<T>::iterator last)
{
// 정렬
quick_sort<T>(begin, last);
// 가운데(median) 원소 반복자를 반환
return begin + (std::distance(begin, last) / 2);
}
퀵 정렬때와 다르게, 피봇 위치 반복자를 인자로 받는 형태로 분할 함수를 만들어 사용한다
template <typename T>
auto partition_using_given_pivot(typename std::vector<T>::iterator begin,
typename std::vector<T>::iterator end,
typename std::vector<T>::iterator pivot)
{
// 피벗 위치는 함수 인자로 주어지므로,
// 벡터의 시작과 마지막 원소를 가리키는 반복자를 정의합니다.
auto left_iter = begin;
auto right_iter = end;
while (true)
{
// 벡터의 첫 번째 원소부터 시작하여 피벗보다 큰 원소를 찾습니다.
while (*left_iter < *pivot && left_iter != right_iter)
left_iter++;
// 벡터의 마지막 원소부터 시작하여 역순으로 피벗보다 작은 원소를 찾습니다.
while (*right_iter >= *pivot && left_iter != right_iter)
right_iter--;
// 만약 left_iter와 right_iter가 같다면 교환할 원소가 없음을 의미합니다.
// 그렇지 않으면 left_iter와 right_iter가 가리키는 원소를 서로 교환합니다.
if (left_iter == right_iter)
break;
else
std::iter_swap(left_iter, right_iter);
}
if (*pivot > *right_iter)
std::iter_swap(pivot, right_iter);
return right_iter;
}
선형 시간 검색 알고리즘을 다음과 같이 구현한다
// 벡터 V에서 i번째로 작은 원소 찾기
template<typename T>
typename std::vector<T>::iterator linear_time_select(
typename std::vector<T>::iterator begin,
typename std::vector<T>::iterator last,
size_t i)
{
auto size = std::distance(begin, last);
if (size > 0 && i < size)
{
// 5개 원소로 구분하여 만들 부분 벡터 Vi의 개수 계산
auto num_Vi = (size + 4) / 5;
size_t j = 0;
// 각각의 Vi에서 중앙값을 찾아 벡터 M에 저장
std::vector<T> M;
for (; j < size / 5; j++)
{
auto b = begin + (j * 5);
auto l = begin + (j * 5) + 5;
M.push_back(*find_median<T>(b, l));
}
if (j * 5 < size)
{
auto b = begin + (j * 5);
auto l = begin + (j * 5) + (size % 5);
M.push_back(*find_median<T>(b, l));
}
// Vi의 중앙값으로 구성된 벡터 M에서 다시 중앙값 q를 찾음
auto median_of_medians = (M.size() == 1) ? M.begin() :
linear_time_select<T>(M.begin(), M.end() - 1, M.size() / 2);
// 분할 연산을 적용하고 피벗 q의 위치 k를 찾음
auto partition_iter = partition_using_given_pivot<T>(begin, last, median_of_medians);
auto k = std::distance(begin, partition_iter) + 1;
if (i == k)
return partition_iter;
else if (i < k)
return linear_time_select<T>(begin, partition_iter - 1, i);
else if (i > k)
return linear_time_select<T>(partition_iter + 1, last, i - k);
}
else
{
return begin;
}
}
테스트 함수
template <typename T>
void print_vector(std::vector<T> arr)
{
for (auto i : arr)
std::cout << i << " ";
std::cout << std::endl;
}
void run_linear_select_test()
{
std::vector<int> S1 {45, 1, 3, 1, 2, 3, 45, 5, 1, 2, 44, 5, 7};
std::cout << "입력 벡터:" << std::endl;
print_vector<int>(S1);
std::cout << "정렬된 벡터:" << std::endl;
print_vector<int>(merge_sort<int>(S1));
std::cout << "3번째 원소: " << *linear_time_select<int>(S1.begin(), S1.end() - 1, 3) << std::endl;
std::cout << "5번재 원소: " << *linear_time_select<int>(S1.begin(), S1.end() - 1, 5) << std::endl;
std::cout << "11번째 원소: " << *linear_time_select<int>(S1.begin(), S1.end() - 1, 11) << std::endl;
}
정리
- linear_time_select()함수는 입력 벡터 V에 대해 분할 연산을 수행하고, 분할된 부분 벡터 중 하나에 대해서만 재귀적으로 자기 자신을 호출한다.
- 매 번 재귀 호출이 일어날 때 마다 벡터 크기가 적어도 30% 줄어든다.
- 이 알고리즘에 의한 재귀 방정식을 풀어서 시간 복잡도를 구해보면 O(n)이 된다.
- 입력 벡터 V를 다섯 개의 원소로 구성된 부분 벡터들로 분할할 때 점근적 선형 복잡도가 달성된다.
- 더 나은 점근적 시간 복잡도를 얻을 수 있는 부분 벡터 크기 결정 방법은 여전히 미해결이다
Ref) 코딩 테스트를 위한 자료 구조와 알고리즘 with C++
Ref) 알기쉬운 알고리즘
'Computer Science > Algorithm' 카테고리의 다른 글
| [Algorithm/Divide&Conquer] 07. 최근접 점의 쌍(Closest Pair) 문제 (0) | 2024.07.02 |
|---|---|
| [Algorithm/Divide&Conquer] 06. 분할 정복 기법과 C++ 표준 라이브러리 함수 (0) | 2024.07.02 |
| [Algorithm/Divide&Conquer] 04. Quick Sort(퀵 정렬) (0) | 2024.07.01 |
| [Algorithm/Divide&Conquer] 03. Merge Sort(병합 정렬) (0) | 2024.07.01 |
| [Algorithm/Divide&Conquer] 02. 이진 검색(binary search) (0) | 2024.07.01 |