해시 테이블에서 충돌
- 다수의 키를 저장할 수 없는 문제를 해결해보자
체이닝
- 앞에서는 하나의 해시 값에 대해 하나의 원소만을 저장했다.
- 따라서 특정 해시 값 위치에 이미 원소가 존재한다면 새로운 값과 예전 값 중 하나를 버릴 수밖에 없었다.
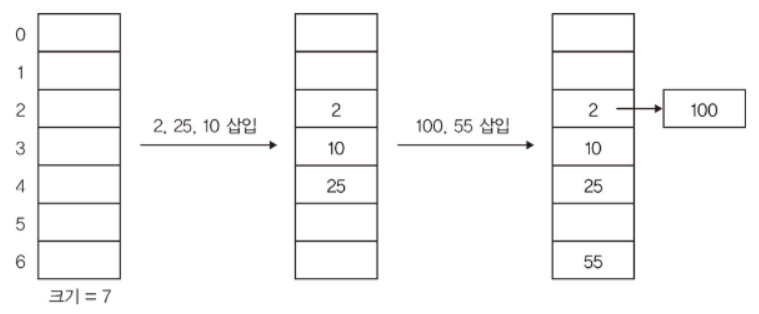
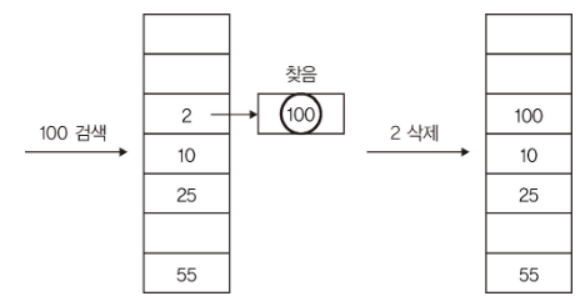
체이닝(chaining)은 두 값을 모두 저장할 수 있는 여러 방법 중 하나이다
- 이 방법은 해시 테이블의 특정 위치에서 하나의 키를 저장하는 것이 아니라, 하나의 연결 리스트를 저장한다
- 새로 삽입된 키에 의해 충돌이 발생하면, 리스트의 맨 뒤에 새로운 키를 추가한다
- 따라서 다수의 원소를 원하는 만큼 저장할 수 있다
- 벡터 대신 연결 리스트를 사용하는 이유는, 특정 위치의 원소를 빠르게 삭제하기 위함이다
Example) 체이닝을 사용하는 해시 테이블
#include <iostream>
#include <vector>
#include <list>
#include <algorithm>
using uint = unsigned int;
class hash_map
{
std::vector<std::list<int>> data;
public:
// 해시 맵 또는 데이터의 크기를 인자로 받는 생성자
hash_map(size_t n)
{
data.resize(n);
}
// 삽입 함수
void insert(uint value)
{
int n = data.size();
data[value % n].push_back(value);
std::cout << value << "을(를) 삽입했습니다." << std::endl;
}
// 검색 함수
bool find(uint value)
{
int n = data.size();
auto& entries = data[value % n];
return std::find(entries.begin(), entries.end(), value) != entries.end();
}
// 삭제 함수
void erase(uint value)
{
int n = data.size();
auto& entries = data[value % n];
auto iter = std::find(entries.begin(), entries.end(), value);
if(iter != entries.end())
{
entries.erase(iter);
std::cout << value << "을(를) 삭제했습니다." << std::endl;
}
}
};
int main()
{
hash_map map(7);
auto print = [&](int value) {
if(map.find(value))
std::cout << "해시 맵에서 " << value << "을(를) 찾았습니다.";
else
std::cout << "해시 맵에서 " << value << "을(를) 찾지 못했습니다.";
std::cout << std::endl;
};
map.insert(2);
map.insert(25);
map.insert(10);
map.insert(100);
map.insert(55);
print(100);
print(2);
map.erase(25);
return 0;
}

- 룩업 함수는 아무래도 이전 구현보다는 살짝 느리다.
- 이 함수는 단순히 n 값에 영향을 받는 것이 아니라, 입력 데이터에도 영향을 받는다
- 삽입 함수의 시간 복잡도는 O(1)이다.
- 리스트에 노드를 추가하는 연산이 단순히 값을 설정하는 것 보다는 조금 느릴 수 있지만 심하게 느리지는 않다.
- 체이닝을 통해 얻을 수 있는 이점에 비하면 무시할 수 있는 수준이다.
- 룩업과 삭제는 데이터 크기와 헤시 테이블의 크기에 따라 상당히 느릴 수 있다.
- 예를 들어 모든 키가 같은 해시 값을 가질 경우, 룩업 연산은 연결 리스트에서 선형 검색 수행과 같으므로 O(N)의 시간 복잡도를 갖는다
- 해시 테이블이 저장할 키 개수에 비해 매우 작다면 충돌이 많이 발생하게 되고, 리스트는 평균적으로 더 길어진다
- 반대로 너무 큰 해시 테이블을 가지고 있다면 메모리 낭비가 발생한다
- 응용 프로그램 동작 시나리오를 고려하여 해시 테이블 크기를 적절히 조절해야 한다
- 예를 들어 모든 키가 같은 해시 값을 가질 경우, 룩업 연산은 연결 리스트에서 선형 검색 수행과 같으므로 O(N)의 시간 복잡도를 갖는다
- 부하율(load factor)는 해시 테이블에서 각각의 리스트에 저장되는 키의 평균 개수를 나타내며, 다음 수식을 이용하여 구할 수 있다
- 부하율 = 전체 키 개수 / 해시 테이블의 크기
- 만약 키 개수가 해시 테이블의 크기와 같다면 부하율은 1이다.
- 부하율이 1보다 작으면 리스트 당 키가 하나도 저장되지 않은 경우가 있다는 것이고, 이는 메모리 낭비가 될 수 있다
- 부하율이 1보다 크면 리스트의 평균 길이가 1보다 크다는 의미이고, 이 경우 검색, 삭제 등의 함수가 약간 느리게 동작할 수 있다
- 이는 매우 이상적인 상태로, 모든 연산이 O(1)에 가깝게 작동하고 모든 메모리 공간을 적절하게 활용한다
- 부하율은 항상 O(1)의 시간 복잡도로 계산할 수 있다
- 몇몇 해시 테이블은 부하율이 1 근방의 특정 값보다 너무 크거나 작아지면 해시 함수를 변경하도록 구현되어 있으며, 이를 재해싱(rehashing)이라고 한다.
- 즉, 해시 함수를 수정하여 부하율이 1에 가까운 값이 되도록 만드는 것이다.
- 변경된 해시 함수에 의한 값의 분포와 부하율을 고려하여 해시 테이블의 크기도 변경할 수 있다.
- 부하율이 해시 테이블의 성능을 결정하는 유일한 지표는 아니다
- ex) 크기가 7인 해시 테이블에 일곱 개의 원소가 저장되어 있는데, 모든 원소가 같은 해시 값을 가져서 하나의 버킷에 있다.
- 여기서 버킷이란 해시 테이블의 한 셀 또는 한 셀에 연결되어 있는 하나의 연결 리스트를 나타낸다
- 검색 연산이 항상 O(1)이 아닌 O(N)의 시간 복잡도를 갖지만, 부하율은 1로 계산되버린다
- 위 경우 해시 함수가 문제이다.
- 해시 함수는 서로 다른 키가 가급적이면 겹치지 않고 골고루 분포되도록 해시 값을 만들어야 한다.
- 기본적으로 버킷의 최대 크기와 최소 크기의 차이가 너무 크면 좋지 않다.
- 위 예시에서는 차이가 7이다
- 만약 해시 함수가 전체 일곱 개의 원소에 대해 서로 다른 해시 값을 반환한다면 검색 함수의 시간 복잡도는 O(1)이다.
- 이 때 최대, 최소 버킷 크기 차이는 0이다
- 이렇게 만드는 작업은 해시 테이블 구현에서 수행되지 않고, 해시 함수 자체에서 잘 고려해야 한다.
- 해시 테이블은 해시 함수 구현에 종속적이지 않기 때문이다
- ex) 크기가 7인 해시 테이블에 일곱 개의 원소가 저장되어 있는데, 모든 원소가 같은 해시 값을 가져서 하나의 버킷에 있다.
열린 주소 지정(open addressing)
충돌을 해결하는 다른 방법으로 열린 주소 지정(open addressing)이 있다.
- 이 방법은 체이닝처럼 해시 테이블에 추가적인 리스트를 붙여서 데이터를 저장하는 방식이 아니라, 모든 원소를 해시 테이블 내부에 저장하는 방식이다
- 따라서 해시 테이블의 크기가 반드시 데이터 개수보다 커야 한다
- 열린 주소 지정 방법의 핵심은 특정 해시 값에 해당하는 위치가 이미 사용되고 있다면, 테이블의 다른 비어 있는 위치를 탐색하는 것이다
선형 탐색(linear probing)
- 가장 간단한 탐색 방법으로, 특정 해시 값에서 충돌이 발생하면 해당 위치에서 하나씩 다음 셀 위치로 이동하면서 셀이 비어 있는지를 확인하고, 비어 있는 셀을 찾으면 원소를 삽입한다.
- 즉 hash(x)에 해당하는 셀이 이미 채워져 있다면 hash(x + 1) 위치의 셀을 확인한다.
- hash(x + 1) 도 사용중이라면 hash(x + 2) 셀을 검사한다
- 즉 hash(x)에 해당하는 셀이 이미 채워져 있다면 hash(x + 1) 위치의 셀을 확인한다.
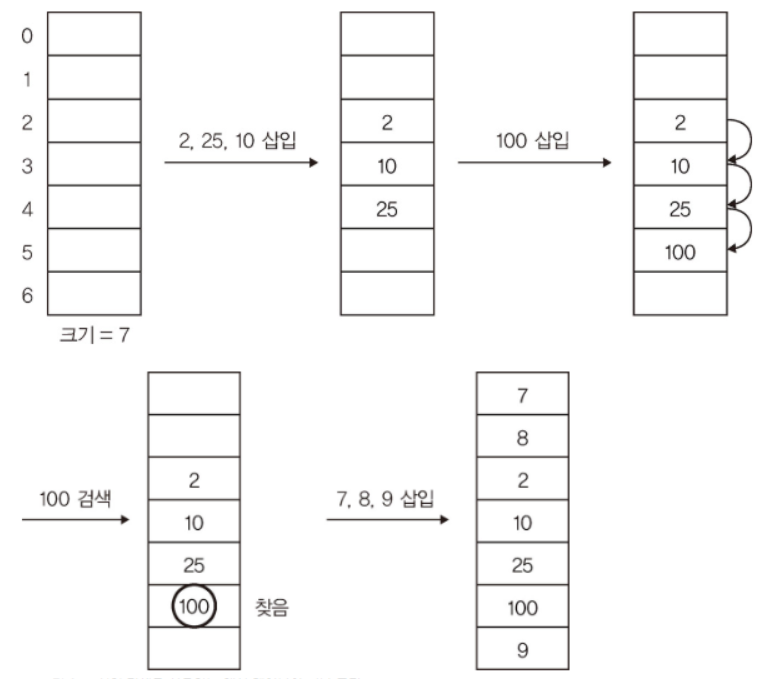
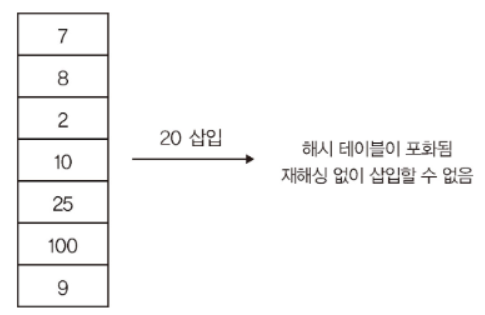
- 해시 테이블이 가득 차서 포화된 경우 재해싱 없이 새 원소를 삽입할 수 없다
- 위 예시에서 보면 해시 테이블의 서로 인접한 군집 형태로 값이 채워졌다
- 만약 원소 검색을 할 경우, 해시 함수에서 반환된 위치가 큰 군집의 시작 위치를 가리킨다면 클러스터의 맨 마지막 위치까지 선형 검색을 해야 한다
- 이 경우 검색 속도가 크게 느려질 수 있다
- 즉, 데이터가 특정 위치에 군집화(clustering)되는 경우에 문제가 발생하게 된다
- 특정 해시 값이 너무 자주 발생해서 데이터가 몇 개의 그룹으로 뭉치는 형태로 저장된다는 의미이다
이차함수 탐색(quadratic probing)
- 군집화 문제를 해결하기 위해 선형 방정식이 아닌 이차 방정식을 사용하여 탐색을 수행할 수 있다.
- 이를 이차함수 탐색 이라고 한다
- hash(x) 위치가 이미 사용중이라면, hash(x + 1^2)으로 이동하고, 그 다음은 hash(x + 2^2)의로 이동한다.
- 이처럼 이동 폭을 이차함수 형태로 증가시키면 데이터 군집이 나타날 확률은 상대적으로 줄어든다
- 선형 탐색 및 이차함수 탐색은 모두 원소 위치가 기존에 삽입되어 있는 다른 원소들에 의해 영향을 받는다
- 이 때 기존에 저장되어 있던 원소는 새로 삽입하는 원소와 서로 다른 해시 값을 가질 수 있다
뻐꾸기 해싱(cuckoo hashing)
뻐꾸기 해싱(cuckoo hashing)은 완벽한 해싱 기법 중 하나이다. 앞서 언급했던 방법들은 최악의 상황에서는 O(1)의 시간 복잡도를 보장하지 않지만, 뻐꾸기 해싱은 구현만 제대로 한다면 O(1)을 만족한다
- 뻐꾸기 해싱은 크기가 같은 두 개의 해시 테이블을 사용하고, 각각의 해시 테이블은 서로 다른 해시 함수를 가진다
- 모든 원소는 두 해시 테이블 중 하나에 있을 수 있으며, 그 위치는 해당 해시 테이블의 해시 함수에 의해 결정된다
이전 해싱 기법과 다른점
- 원소가 두 해시 테이블 중 어디든 저장될 수 있다
- 원소가 나중에 다른 위치로 이동할 수 있다
- 앞서 언급한 해싱 방법에서는 재해싱을 수행하지 않는 한 원소가 최초 삽입된 위치에서 다른 위치로 이동할 수 없다
- 그러나 뻐구기 해싱 방법에서는 모든 원소가 두 개의 저장 가능한 위치를 가지며, 상황에 따라 이동할 수 있다
- 상황에 따라 저장 가능한 위치 개수를 증가시킬 수도 있다
- 룩업의 경우 특정 원소가 존재하는지 알기 위해 저장 가능한 위치 두 군데만 확인해보면 되므로, 룩업 연산의 시간 복잡도는 항상 O(1)이다.
- 삽입 연산은 좀 더 오래걸릴 수 있다
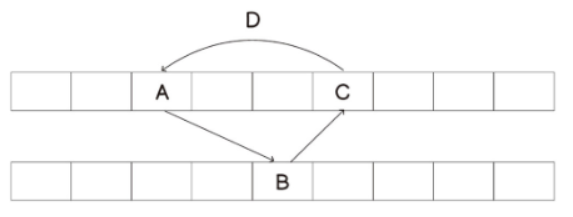
- ex) A라는 원소를 삽입하는 경우, A를 삽입할 해당 위치가 비어있다면 그대로 A를 삽입하면 된다
- 이미 다른 원소 B가 저장되어 있다면, 해당 위치에 A를 저장하고 B를 두 번째 해시 테이블로 옮긴다
- 만약 B가 이동할 위치에 이미 다른 원소 C가 저장되어 있다면 해당 위치에 B를 저장하고 C를 첫 번째 해시 테이블로 옮긴다
- 이러한 작업을 완전히 비어 있는 셀이 나타날 때 까지 재귀적으로 반복한다

- 위와 같은 과정에서 만약 순환이 발생한다면 무한 루프에 빠질 수 있다
- 순환이 발생했다면 새로운 해시 함수를 이용하여 재해싱을 수행해야 한다
- 재해싱 하고도 순환이 발생하여, 여러번 재해싱을 수행해야 할 수도 있다.
- 적절한 해시 함수를 사용하면 높은 확률로 O(1)의 성능을 갖는 해시 테이블을 구성할 수 있다
- 뻐구기 해싱도 전체 해시 테이블 크기 이상의 원소를 저장할 수는 없다
- 높은 성능을 보장하려면 부하율이 0.5보다 작게끔 설정해야 한다
- 즉, 전체 원소 개수가 해시 테이블 크기의 절반보다 작아야 한다
Example) 뻐구기 해싱
#include <iostream>
#include <vector>
using namespace std;
class hash_map
{
// 두 개의 해시 테이블과 각 테이블의 크기
std::vector<int> data1;
std::vector<int> data2;
int size;
// 해시 함수 정의
int hash1(int key) const
{
return key % size;
}
int hash2(int key) const
{
return (key / size) % size;
}
public:
// 해시 테이블을 모두 -1로 초기화
hash_map(int n) : size(n)
{
data1 = std::vector<int>(size, -1);
data2 = std::vector<int>(size, -1);
}
// 룩업 함수
// 양쪽 해시 테이블에서 키를 검색하고 해당 위치에 나타내는 반복자 바노한
std::vector<int>::iterator lookup(int key)
{
auto hash_value1 = hash1(key);
if(data1[hash_value1] == key)
{
std::cout << "1번 테이블에서 " << key << "을(를) 찾았습니다." << std::endl;
return data1.begin() + hash_value1;
}
auto hash_value2 = hash2(key);
if(data2[hash_value2] == key)
{
std::cout << "2번 테이블에서 " << key << "을(를) 찾았습니다." << std::endl;
return data2.begin() + hash_value2;
}
return data2.end();
}
void erase(int key)
{
auto position = lookup(key);
if(position != data2.end())
{
*position = -1;
std::cout << key << "에 해당하는 원소를 삭제했습니다." << std::endl;
}
else
{
std::cout << key << "키를 찾지 못했습니다." << std::endl;
}
}
// 삽입 함수
void insert(int key)
{
insert_impl(key, 0, 1);
}
// 삽입 구현 함수
// key : 키, cnt : 재귀 호출 횟수, table : 키를 삽입할 테이블 번호
void insert_impl(int key, int cnt, int table)
{
if(cnt >= size)
{
std::cout << key << " 삽입 시 순환 발생! 재해싱이 필요합니다!" << std::endl;
return;
}
if(table == 1)
{
int hash = hash1(key);
if(data1[hash] == -1)
{
std::cout << table << "번 테이블에 " << key << " 삽입" << std::endl;
data1[hash] = key;
}
else
{
int old = data1[hash];
data1[hash] = key;
std::cout << table << "번 테이블에 " << key << "삽입 : 기존의 " << old << " 이동 -> ";
insert_impl(old, cnt + 1, 2);
}
}
else
{
int hash = hash2(key);
if(data2[hash] == -1)
{
std::cout << table << "번 테이블에 " << key << " 삽입" << std::endl;
data2[hash] = key;
}
else
{
int old = data2[hash];
data2[hash] = key;
std::cout << table << "번 테이블에 " << key << "삽입 : 기존의 " << old << " 이동 -> ";
insert_impl(old, cnt + 1, 1);
}
}
}
void print()
{
std::cout << "Index : ";
for(int i = 0; i < size; i++)
std::cout << i << '\t';
std::cout << std::endl;
std::cout <<"Data1 : ";
for(auto i : data1)
std::cout << i << '\t';
std::cout << std::endl;
std::cout <<"Data2 : ";
for(auto i : data2)
std::cout << i << '\t';
std::cout << std::endl;
}
};
int main()
{
hash_map map(7);
map.print();
std::cout << std::endl;
map.insert(10);
map.insert(20);
map.insert(30);
std::cout << std::endl;
map.insert(104);
map.insert(2);
map.insert(70);
map.insert(9);
map.insert(90);
map.insert(2);
map.insert(7);
std::cout << std::endl;
map.print();
std::cout << std::endl;
// 순환 발생
map.insert(14);
return 0;
}
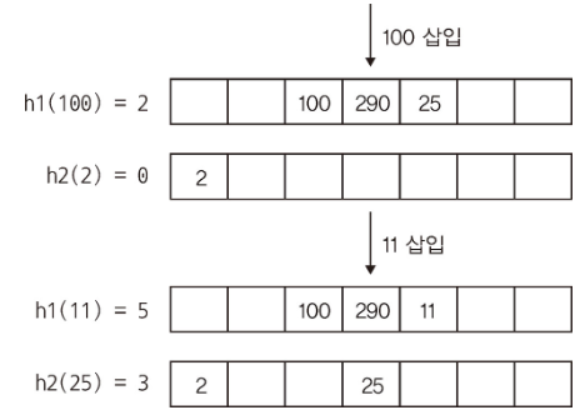

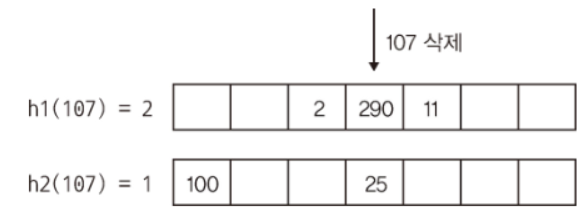
- 룩업 함수는 양쪽 해시 테이블에서 키를 검색하고, 해당 위치를 나타내는 반복자를 반환한다
- 삭제 함수에서 이 반복자를 사용한다
- 원소를 찾지 못하면 data2 테이블의 마짐가을 가리키는 반복자가 반환된다
- O(1)의 시간 복잡도를 갖는다
- 삭제 함수의 경우 룩업 함수가 반환한 값을 조사하여 실제 삭제 작업을 수행하거나, 단순히 문자열만 출력한다
- O(1)
- 삽입은 재귀적으로 동작해야 하기 때문에 삽입 구현 함수를 따로 만든다
- 삽입 함수에서는 순환 여부를 검색해야 한다
- 그러나 방문한 위치의 모든 값을 기억하는 것은 부담이 클 수 있다
- 그러므로 여기서 단순히 재귀 호출 횟수가 몇 회 이상이 되면 순환으로 간주하여 구현한다
- 이 때 최대 재귀 호출 횟수는 해시 테이블의 크기와 같게 설정하였다
- 원소 삽입에서만 어느 정도 시간을 필요로 하므로, 위 구현 코드는 원소 삽입보다 룩업 연산이 훨씬 많은 application에서 적합하다
'Data Structure > 자료구조' 카테고리의 다른 글
| [자료구조] 블룸 필터(bloom filter) (0) | 2024.06.23 |
|---|---|
| [자료구조] 해시 테이블(1) (0) | 2024.06.23 |
| [자료구조] 다양한 트리구조(균형 트리, N-항 트리) (0) | 2024.06.18 |
| [자료구조] 다양한 트리 구조(BST) (0) | 2024.06.18 |
| [자료구조] 비선형 문제 (0) | 2024.06.18 |