다양한 트리 구조(BST)
- 평범한 이진 트리의 효용성은 그리 높지 않음
- BST, Balanced Tree 등에 대해 알아보자
이진 검색 트리(BST, Binary Search Tree)
- 널리 사용되는 형태의 이진 트리
- 다음과 같은 속성이 있다.
- 부모 노드의 값 >= 왼쪽 자식 노드의 값
- 부모 노드의 값 <= 오른쪽 자식 노드의 값
- 즉, (왼쪽 노드 <= 부모 노드 <= 오른쪽 노드) 관계를 갖는다
- 부모 노드보다 작거나 같은 모든 원소는 항상 왼쪽에 있다.
- 부모 노드보다 크거나 같은 원소는 항상 오른쪽에 있다.
완전 이진 트리(complete binary tree)
- 이진트리에서 마지막 레벨을 제외한 모든 노드에 두개의 자식 노드가 있는 트리를 말함
- 이 때 트리의 높이는 log_2(N)이 됨
BST에서 원소 검색
- BST의 속성 때문에 원소 검색을 위해 루트 노드부터 차례대로 값을 비교하는 경우, 각 단계마다 검색 범위가 절반으로 줄어든다
- 완전 이진 트리의 검색 및 삽입 동작은 O(logN)의 시간 복잡도를 갖는다.
- 이진 트리의 검색 및 삽입 동작은 정확히는 O(logN)의 시간 복잡도를 갖는다고 보기 어렵다.
- 정확한 시간 복잡도는 아래에서 다시 다룰거에요
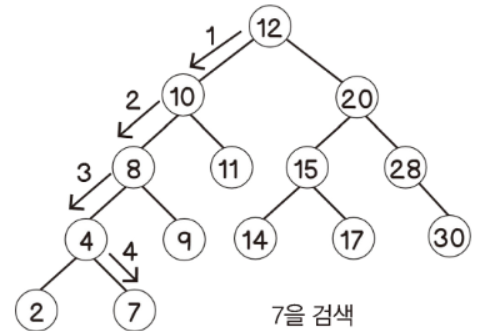
EX) 아래와 같이 중복되지 않는 양수를 원소로 갖는 트리가 있으며, 7을 찾아보자
- 루트 노드 부터 비교하여 어느쪽 하위 노드로 이동해야 할 지 결정하고, 계속 이동하면서 검색하고자 하는 값과 일치하는 노드를 찾는다.
- BST에서 원소를 검색할 때는 트리의 모든 원소를 방문하지 않아도 됨
- 현재 노드가 찾고자 하는 노드가 아닐 때마다 검색 범위가 반으로 줄어듬
- 선형 자료 구조, 특히 분할 정복과 유사함
BST에서 새 원소 삽입하기

- 먼저 원소가 삽입될 위치의 부모 노드를 찾아야 함
- 루트 노드부터 시작하여 각 노드를 추가할 원소와 비교하면서 원소가 삽입될 위치로 이동해야 한다
BST에서 원소 삭제하기

- 단순히 노드 삭제하는 것으로 끝나지 않고, 노드 삭제 후 전체 트리가 BST 속성을 만족하도록 다른 적절한 노드로 삭제된 노드를 대체해야 한다
- 삽입보다 복잡하다
3가지 Case
- 자식 노드가 없는 경우 : 단순히 해당 노드를 삭제한다
- 자식 노드가 하나만 있는 경우, 노드 삭제 후, 부모 노드의 포인터가 해당 자식 노드를 가리키도록 조정
- 자식 노드가 두 개 있는 경우 : 노드 삭제 후, 현재 노드를 후속 노드(successor)로 대체한다
(여기서 후속 노드란 현재 노드 다음으로 큰 숫자를 가진 노드를 말함)
현재 노드를 후속 노드로 대체하는 과정
- 현재 노드의 오른쪽 서브 트리로 이동한 후, 여기서 가장 작은 값의 노드를 찾으면 된다
- 가장 작은 값의 노드를 찾으려면, 서브 트리에서 가장 왼쪽에 위치한 노드로 이동하면 된다
- 후속 노드는 오른쪽 자식 노드 하나만 가질 수 있다.
- 왼쪽 자식이 있었다면 그 노드를 후속 노드로 선택했을 것이기 때문
트리 연산의 시간 복잡도
- 검색
- 이론적으로는 매번 검색 범위가 절반적으로 줄어듬
- N개의 노드를 가지고 있는 BST에서 검색에 필요한 시간
- T(N) = T(N/2) + 1
- 따라서 T(N) = O(log N)
- 주의해야 하는 점!
- 트리의 모양이 원소 삽입 순서에 따라 결정된다
- 검색 범위가 T(N/2) 형태로 항상 줄어드는 것도 아니다
- 따라서 시간 복잡도가 O(log N)이라는 것도 항상 정확하다고 볼 수 없다
- 검색 범위가 T(N/2) 형태로 항상 줄어드는 것도 아니다
- 트리의 모양이 원소 삽입 순서에 따라 결정된다
BST 구현
#include <iostream>
struct node
{
int data;
node* left;
node* right;
};
struct bst
{
node* root = nullptr;
node* find(int value)
{
return find_impl(root, value);
}
void insert(int value)
{
if(!root)
root = new node {value, NULL, NULL };
else
insert_impl(root, value);
}
void inorder()
{
inorder_impl(root);
}
node* successor(node* start)
{
auto current = start->right;
while(current && current->left)
current = current->left;
return current;
}
void deleteValue(int value)
{
root = delete_impl(root, value);
}
private:
node* find_impl(node* current, int value)
{
if(!current)
{
std::cout << std::endl;
return NULL;
}
if(current->data == value)
{
std::cout << value << "을(를) 찾았습니다." << std::endl;
return current;
}
// value 값이 현재 노드 왼쪽에 있는 경우
if(value < current->data)
{
std::cout << current->data <<"에서 왼쪽으로 이동 : ";
return find_impl(current->left, value);
}
// value 값이 현재 노드 오른쪽에 있는 경우
std::cout << current->data << "에서 오른쪽으로 이동 : ";
return find_impl(current->right, value);
}
void insert_impl(node* current, int value)
{
if(value < current->data)
{
if(!current->left)
current->left = new node {value, NULL, NULL};
else
insert_impl(current->left, value);
}
else
{
if(!current->right)
current->right = new node {value, NULL, NULL};
else
insert_impl(current->right, value);
}
}
void inorder_impl(node* start)
{
if(!start)
return;
// 왼쪽 서브 트리 방문
inorder_impl(start->left);
// 현재 노드 출력
std::cout << start->data << " ";
// 오른쪽 서브 트리 방문
inorder_impl(start->right);
}
node* delete_impl(node* start, int value)
{
if(!start)
return NULL;
if(value < start->data)
start->left = delete_impl(start->left, value);
else if(value > start->data)
start->right = delete_impl(start->right, value);
else
{
// 자식 노드가 전혀 없거나, 왼쪽 자식 노드만 없는 경우
if(!start->left)
{
auto tmp = start->right;
delete start;
return tmp;
}
// 오른쪽 자식 노드만 없는 경우
if(!start->right)
{
auto tmp = start->left;
delete start;
return tmp;
}
// 자식 노드 둘 다 있는 경우
auto succNode = successor(start);
start->data = succNode->data;
// 오른쪽 서브 트리에서 후속(successor)을 찾아 삭제
start->right = delete_impl(start->right, succNode->data);
}
return start;
}
};
using namespace std;
int main()
{
bst tree;
tree.insert(12);
tree.insert(10);
tree.insert(20);
tree.insert(8);
tree.insert(11);
tree.insert(15);
tree.insert(28);
tree.insert(4);
tree.insert(2);
std::cout << "중위 순회 : ";
tree.inorder();
std::cout << std::endl;
tree.deleteValue(12);
std::cout << "12를 삭제한 후 중위 순회 : ";
tree.inorder();
std::cout << endl;
if(tree.find(12))
std::cout << "원소 12는 트리에 있습니다." << std::endl;
else
std::cout << "원소 12는 트리에 없습니다." << std::endl;
return 0;
}'Data Structure > 자료구조' 카테고리의 다른 글
| [자료구조] 해시 테이블(1) (0) | 2024.06.23 |
|---|---|
| [자료구조] 다양한 트리구조(균형 트리, N-항 트리) (0) | 2024.06.18 |
| [자료구조] 비선형 문제 (0) | 2024.06.18 |
| [자료구조] 트리 - 분리 집합 (0) | 2024.06.15 |
| [자료구조] 수식 트리 (0) | 2024.06.15 |