거듭 제곱 계산법
- C^2을 계산하기 위해서는 다음과 같이 C 자신을 두 번 곱해야 한다
- C^2 = C X C
- C^n을 계산하려면 C 자신을 n번 곱해야 한다.
- 이를 코드로 바꾸면 다음과 같다
int Power( int Base, int Exponent )
{
int i=0;
int Result = 1; // C^0은 1이므로
for ( i=0; i<Exponent; i++ )
Result *= Base;
return Result;
}
- 지수 크기만큼 곱셈을 수행하므로 O(n) 수행 시간을 소요한다는 사실을 알 수 있다.
- 이보다 더 빠른 방법은 없을까?
접근
- C^8은 C x C x C x C x C x C x C x C 로 정의되지만
- 다음과 같이 표현할 수도 있다.
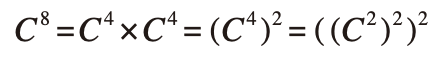
- C^2을 구한 뒤 제곱을 두 번 더 반복하여 결국 세 번의 곱셈만 수행함으로써 같은 결과를 얻을 수 있다.
- 하지만 이 방법을 모든 제곱 연산에 적용할 수는 없다.
- 제곱 수가 홀수인 경우도 있기 때문
- 제곱수가 홀수인 경우 다음 정리를 이용할 수 있다.
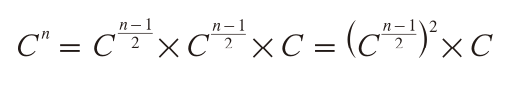
- 이를 이용하여 재귀 방정식을 만들면 다음과 같다
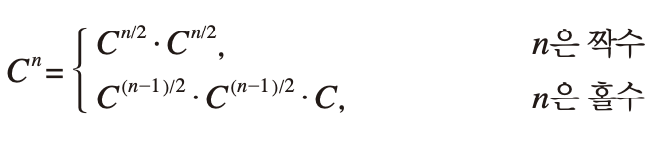
구현
거듭 제곱은 기하 급수적으로 늘어나므로 unsigned long 타입에 저장하기로 하자
typedef unsigned long ULONG; // 64bit
ULONG Power(int Base, int Exponent) {
if (Exponent == 1)
return Base;
else if (Base == 0)
return 1;
if (Exponent % 2 == 0) {
ULONG NewBase = Power(Base, Exponent / 2);
return NewBase * NewBase;
} else {
ULONG NewBase = Power(Base, (Exponent - 1) / 2);
return (NewBase * NewBase) * Base;
}
}
예제 프로그램
#include <stdio.h>
typedef unsigned long ULONG;
ULONG Power( int Base, int Exponent )
{
if ( Exponent == 1 )
return Base;
else if ( Base == 0 )
return 1;
if ( Exponent % 2 == 0 )
{
ULONG NewBase = Power( Base, Exponent/2 );
return NewBase * NewBase;
}
else
{
ULONG NewBase = Power( Base, (Exponent-1)/2 );
return (NewBase * NewBase) * Base;
}
}
int main( void )
{
int Base = 2;
int Exponent = 30;
printf("%d^%d = %lu\n", Base, Exponent, Power( Base, Exponent ));
return 0;
}
참조) 박상현, 『이것이 자료구조+알고리즘이다 with C언어』, 한빛미디어(2022)
'Algorithm > Divide&Conquer' 카테고리의 다른 글
| [Algorithm/Divide&Conquer] 09. 분할 정복을 적용하는데 있어서 주의할 점 (0) | 2024.07.02 |
|---|---|
| [Algorithm/Divide&Conquer] 08. L-트로미노 타일링 (0) | 2024.07.02 |
| [Algorithm/Divide&Conquer] 07. 최근접 점의 쌍(Closest Pair) 문제 (0) | 2024.07.02 |
| [Algorithm/Divide&Conquer] 06. 분할 정복 기법과 C++ 표준 라이브러리 함수 (0) | 2024.07.02 |
| [Algorithm/Divide&Conquer] 05. 선택(selection) 문제, 선형 시간 선택 (0) | 2024.07.01 |