최근접 점의 쌍 문제란?
2차원 평면상의 n개의 점이 입력으로 주어질 때, 거리가 가장 가까운 한 쌍의 점을 찾는 문제

가장 간단한 해결 방법
- 모든 점에 대하여 각각의 두 점 사이의 거리를 계산하여 가장 가까운점의 쌍을 찾다.
- nC2 X O(1) = O(n^2)
- 이것보다 효율적인 방법은 없을까?
분할 정복을 이용한 해결 방법
1. n개의 점을 1/2로 분할하여 각각의 부분 문제에서 최근접 점의 쌍을 찾고, 2개의 부분해 중에서 짧은 거리 (d)를 가진 점의 쌍을 일단 찾는다. (recursive하게 반복하여 구함)
2. [결합] 2개의 부분해를 취합할 때에는 반드시 두 부분 문제서 각각 한 점씩 포함되는 점의 쌍 중에서 그 거리가 d 보다 작은 쌍을 찾는다. (중간영역 고려!)
- 만일 이러한 쌍이 있다면 그런 쌍 중에 가장 짧은 쌍이 해이다.
- 그렇지 않다면, 거리가 d인 쌍이 해이다

중간영역에 있는 (두 점이 서로 다른 부분 문제에 속한) 쌍들을 검색하는 방법
- 점들의 집합을 S라고 하고, S를 둘로 나눈 집합을 S_L , S_R이 라고 하자.
- S_L과 S_R에서 각각 찾은 closest pair를 각각 CPL , CPR이라고 하고, 두 점간의 거리를 dist( ) 함수로 표시하면,
- d = min{dist(CPL), dist(CPR)} = min{10 ,15} =10
- 그러면, 아래 그림에서 보인 것과 같이 분할한 지점에서 x 축으로 ±d인 범위에 속한 점들만 검색하면 충분하다

- S의 점들이 x 좌표로 non-decreasing하게 정렬되어 있다면, 아래의 예로 탐색할 점들의 범위를 설명할 수 있다.
- 아래 배열에는 점들이 x-좌표의 오름차순으로 정렬되어 있고, 각 점의 y-좌표는 생략되었다.
- d =10이라면, 점 (17,-), (25,-), (26,-), (28,-), (30,-), (37,-)이 중간 영역 즉, combine 과정에서 검색할 점들에 속한다.

최근접 점의 쌍 분할 정복 알고리즘 - 슈도 코드
ClosestPair(S)
입력: x-좌표의 오름차순으로 정렬된 배열 S에는 i개의 점 // 𝑂(nlogn), (단, 각 점은 (x,y)로 표현된다.)
출력: S에 있는 점들 중 최근접 점의 쌍의 거리
1. if (i ≤ 3) return (2 또는 3개의 점들 사이의 최근접 쌍) // 점 2or3이면, 𝑂(1)
2. 정렬된 S를 같은 크기의 S_L과 S_R로 분할한다. // index 이용 계산 𝑂(1)
(1) |S|가 홀수이면, |S_L| = |S_R|+1이 되도록 분할한다.
3. CP_L = ClosestPair(S_L) // CP_L은 S_L에서의 최근접 점의 쌍
4. CP_R = ClosestPair(S_R) // CP_R은 S_R에서의 최근접 점의 쌍
5. d = min{dist(CP_L), dist(CP_R)}일 때, 중간 영역에 속하는 점들 중에서 최근
접 점의 쌍을 찾아서 이를 CP_C라고 하자.
6. return (CP_L, CP_C, CP_R 중에서 거리가 가장 짧은 쌍) // 𝑂(1)
중간 영역에서의 CPC 찾기

- n 개의 점을 분할하면 중간 영역에 최대 몇 개의 점이 있을 수 있을까?
- 최악의 경우 SL과 SR의 모든 점들이 중간 영역에 있을 수 있다.
- 따라서, 중간 영역에서 brute force한 방법으로 closest pair 를 찾으면 O(n^2) -> 아무런 이득을 볼 수 없음.
- 어떻게 하는게 좋을까?
- 중간 영역에 있는 점들을 y-좌표 기준으로 오름차순 또는 내림차순으로 정렬해보자.
- y 축으로 내림차순으로 정렬 한 점들을 p1 , p2 , p3 , …, pn 이라고 하자.
- 그리고 점 pi 의 y 좌표를 yi 라고 하자. 점들이 y 방향으로 정렬되어 있으므로, 아래와 같은 방법이 보다 효율적임.
for (i = 1; i <= n-1; i++ )
for ( j = i+1; j <= n; j++ )
if ( yi– yj >= d) break; // 즉, pi - pj > d
dij= dist (pi, pj)를 구하고, dij <d이면 d=dij ;
- 그러나, 위 과정은 d 값에 따라 그 속도가 결정된다.
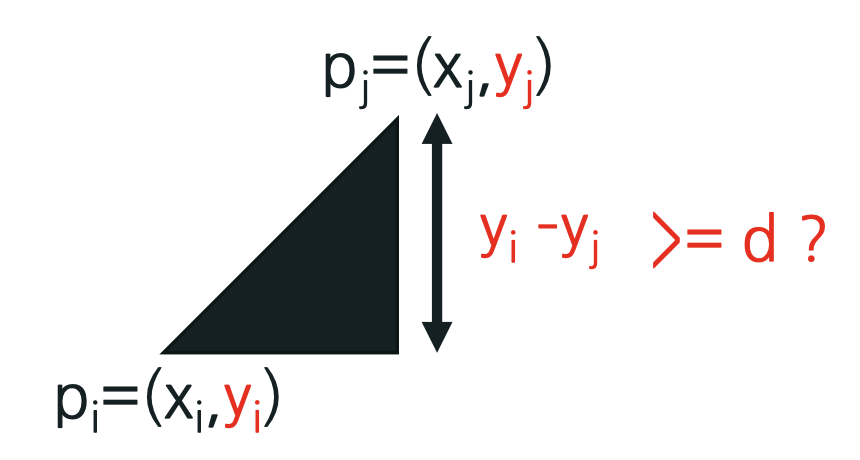
시간 복잡도
입력 S에 n개의 점이 있다고 해보자.
- 전처리 (preprocessing) 과정 : S의 점을 x-좌표로 정렬: 𝑂(nlog n)
- Line 1 : S에 3개의 점이 있는 경우에 3번의 거리 계산이 필요하고, S의 점의 수가 2이면 1번의 거리 계산이 필요하므로 𝑂(1) 시간이 걸린다.
- Line 2 : 정렬된 S를 SL과 SR로 분할하는데, 이미 배열에 정렬되어 있으므로, 배열의 중간 인덱스로 분할하면 된다. 이는 𝑂(1) 시간 걸린다.
- Line 3~4 : SL과 SR에 대하여 각각 ClosestPair를 호출하는데, 분할하며 호출되는 과정은 합병 정렬과 동일
- Line 5 : d = min{dist(CPL), dist(CPR)}일 때 중간 영역에 속하는 점들 중에서 최근접 점의 쌍을 찾는다.
- y-좌표로 정렬하므로 𝑂(nlog n) 시간
- 이후, 아래에서 위로 올라가며 각 점에서 주변의 점들 사이의 거리를 계산하는데 𝑂(1) 시간. 왜냐하면 각 점과 거리 계산해야 하는 주변 점들의 수는 𝑂(1)개이기 때문이다.
- Line 6: 3개의 점의 쌍 중에 가장 짧은 거리를 가진 점의 쌍을 리턴하므로 𝑂(1) 시간이 걸린다
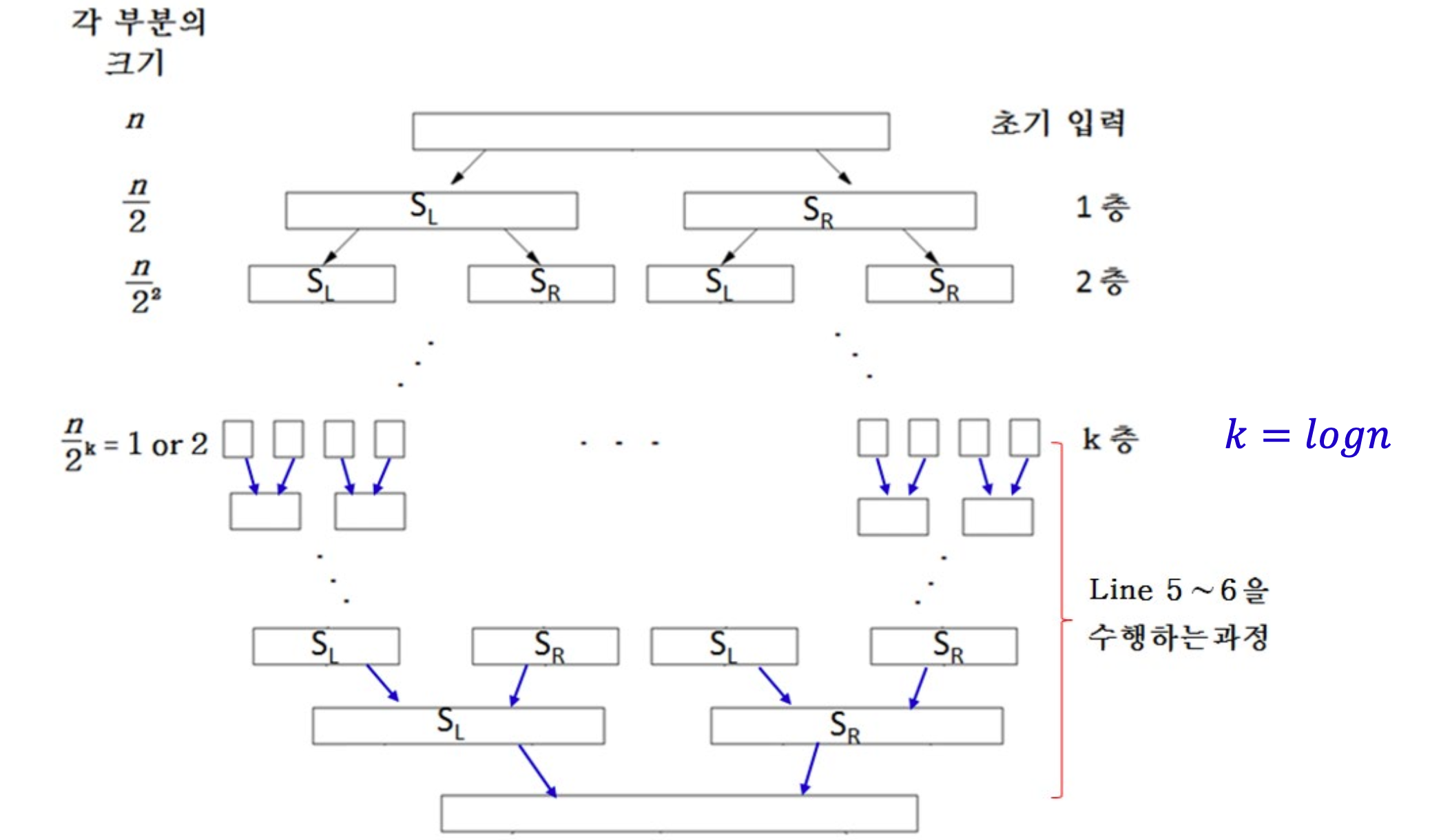
k층까지 분할된 후, 층별로 line 5~6이 수행되는 combine (취합) 과정을 진행하므로
(각 층의 y좌표 정렬 수행 시간) X (층 수) = O(nlog n) X log n = 𝑶(nlog^2 (n))
ClosestPair 알고리즘의 시간복잡도 = 𝑶(nlog^2 (n))이다.
시간복잡도를 O(nlog n)으로 줄이기 위한 알고리즘 개선 방법
입력 점들을 배열 A에 저장하고, A를 x-좌표로 정렬한 후, A의 각 원소에 자신의 배열 인덱스를 저장한다. (이는 먼저 x-좌표로 정렬한 후에 임시 배열에 각 원소를 복사하면서 인덱스도 동시에 저장하면 된다.)
인덱스도 동시에 저장된 배열을 새로운 배열 B에 복사한 후 y-좌표로 정렬한다. 정렬된 후에도 각 원소에는 배열 A의 인덱스가 저장되어 있으므로 중간 영역에 속한 점들의 인덱스 범위 (예를 들어, 배열 A의 인덱스가 5에 11사이)를 이용하여 배열 B에서 골라내면, 알고리즘의 line 5를 정상적으로 수행할 수 있다. 여기서 중간 영역에 속한 점들만 배열 B에서 골라내는데 걸리는 시간은 배열 B의 원소를 한 번씩만 조사하면 되므로 O(n)이다.
Ref) 알기쉬운 알고리즘
'Algorithm > Divide&Conquer' 카테고리의 다른 글
| [Algorithm/Divide&Conquer] 09. 분할 정복을 적용하는데 있어서 주의할 점 (0) | 2024.07.02 |
|---|---|
| [Algorithm/Divide&Conquer] 08. L-트로미노 타일링 (0) | 2024.07.02 |
| [Algorithm/Divide&Conquer] 06. 분할 정복 기법과 C++ 표준 라이브러리 함수 (0) | 2024.07.02 |
| [Algorithm/Divide&Conquer] 05. 선택(selection) 문제, 선형 시간 선택 (0) | 2024.07.01 |
| [Algorithm/Divide&Conquer] 04. Quick Sort(퀵 정렬) (0) | 2024.07.01 |