분할 정복 설계 패러다임
- 효율적인 알고리즘을 설계하기 위한 일반적인 접근 방법이 개발되어 다양한 문제 해결에 사용되고 있다.
- 분할 정복(divide-and-conquer)은 가장 널리 사용되는 알고리즘 설계 패러다임 중 하나이다.
분할 정복 알고리즘이란?
- 주어진 문제를 작은 부분 문제로 나누고, 나줘진 각 부분 문제의 솔루션을 구하고, 각 부분 문제 솔루션을 합쳐서 전체 문제에 대한 솔루션을 구하는 방식
- binary search(이진 탐색), quick sort(퀵 정렬), merge sort(병합 정렬), matrix mulitplication(행렬 곱셈), Fast Fourier Trnasform(고속 푸리에 변환), skyline algorithm(스카이라인 알고리즘) 등에서 사용되는 패러다임이다.
분할 정복 접근
- 주어진 문제의 규모가 커서 한 번에 해결하기 어렵다면 이를 작은 부분 문제로 나눠서 해결하는 방식이다.
- 부분 문제로 나누는 작업을 반복하여 그 해답을 찾고, 그 해답을 합쳐서 처음 문제에 대한 해답을 유도해낸다.
- 크게 3 Step으로 나눌 수 있다.
- 분할(divide): 주어진 문제를 동일한 방식!!으로 해결할 수 있는 여러 부분 문제로 나눈다
- 정복(conquer): 각 부분 문제에 대한 해답을 구한다
- 결합(combine): 각 부분 문제의 해답을 결합하여 전체 문제에 대한 해답을 구한다.
- 전체의 일부에서 구한 해답이 전체에서 구한 해답과 같은 경우 일반적인 분할 정복 접근 방법에서 필요한 결합 과정이 필요하지 않음
- 이는 흔치 않은 경우이다.
- ex) 이진 탐색
- 분할된 입력에 대한 문제를 부분 문제(subproblem)이라고 하고, 부분 문제의 해를 부분해라고 한다.
- 부분 문제는 더 이상 분할할 수 없을 때 까지 계속 분할한다
- 이러한 문제 해결 접근 방법은 하향식 접근방법이라고 한다(Top-down)
주어진 입력을 몇 번 분할해야 할까?
크기가 n인 입력을 3개로 분할하고, 각각 분할된 부분 문제의 크기가 n/2라면, 다음과 같이 문제가 분할된다
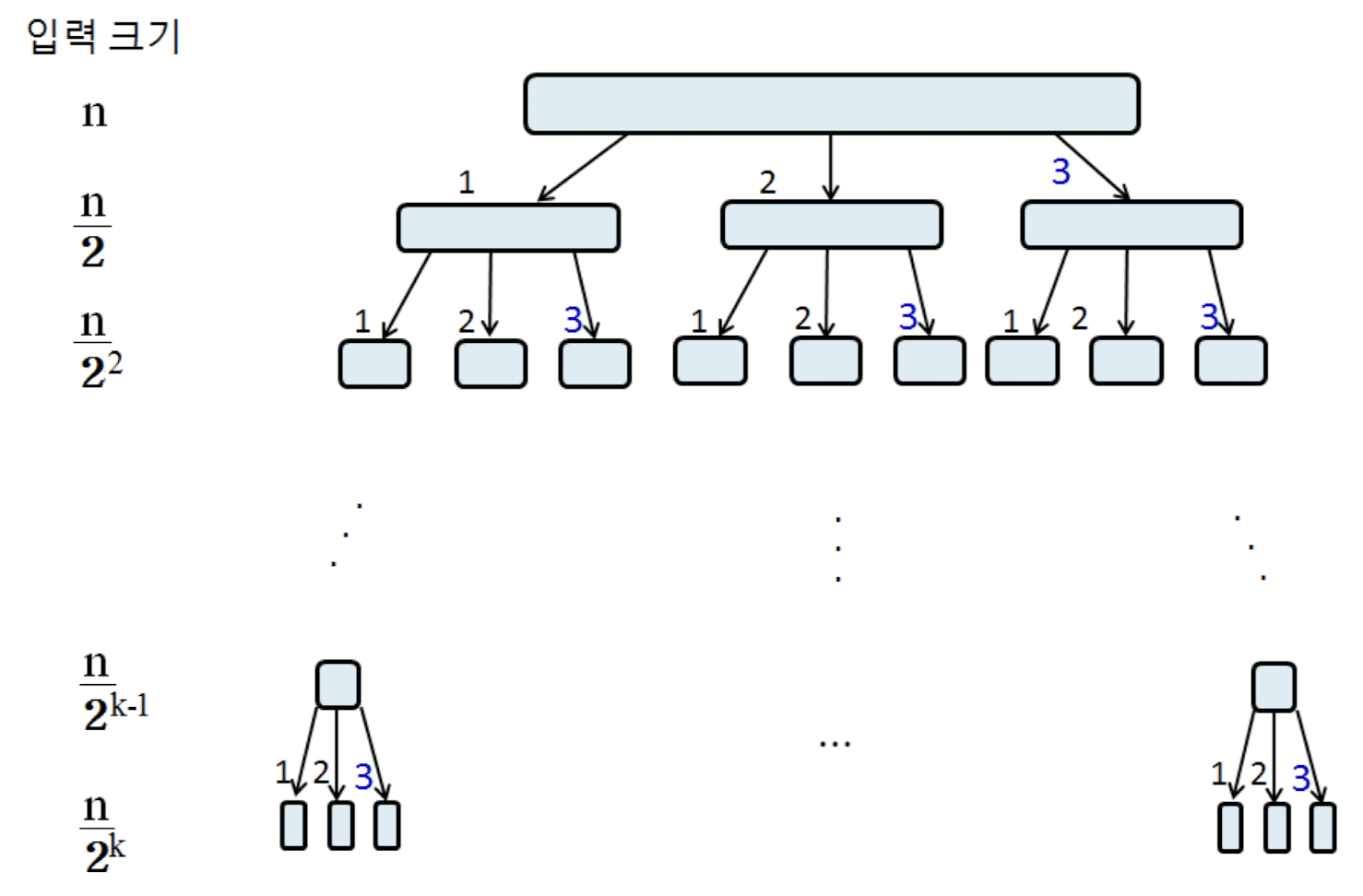
- 총 분할한 횟수를 k라고 하면
- n/(2^k) = 1이므로, k = log_2(n)이다.
Ref) 알기 쉬운 알고리즘(2021)
'Algorithm > Divide&Conquer' 카테고리의 다른 글
| [Algorithm/Divide&Conquer] 06. 분할 정복 기법과 C++ 표준 라이브러리 함수 (0) | 2024.07.02 |
|---|---|
| [Algorithm/Divide&Conquer] 05. 선택(selection) 문제, 선형 시간 선택 (0) | 2024.07.01 |
| [Algorithm/Divide&Conquer] 04. Quick Sort(퀵 정렬) (0) | 2024.07.01 |
| [Algorithm/Divide&Conquer] 03. Merge Sort(병합 정렬) (0) | 2024.07.01 |
| [Algorithm/Divide&Conquer] 02. 이진 검색(binary search) (0) | 2024.07.01 |