수식 트리(Expression Tree)
- 수식 이진 트리(Expression Binary Tree)라고 부르기도 함
- 일반적으로 다음 두가지 규칙을 가짐
- 피연산자는 잎 노드이다.
- 연산자는 뿌리 노드 또는 가지 노드이다.
- ex) 1 * 2 + (7 - 8)의 경우 피연산자 1, 2, 7, 8은 모두 잎 노드, 연산자들은 모두 뿌리 노드 or 가지 노드임
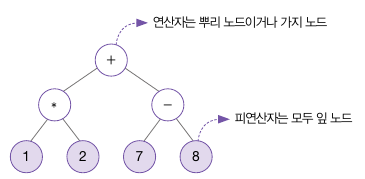
- 뿌리 노드와 가지 노드 모두 피연산자를 양쪽 자식으로 가짐
- 여기서 피연산자는 수(Number)일 수도, 또 다른 식(Expressioin)일 수도 있음
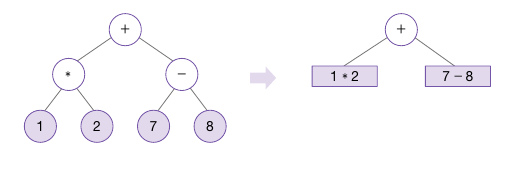
- ex) + 연산자는 하위 트리가 표현하는 수식 (1 * 2)와 (7 - 8)을 피연산자로 가지고 있음
- 수식 트리는 가장 아래에 있는 하위 수식 트리(잎 노드)로 부터 수 또는 계산 결과값을 병합해 올라가는 과정을 반복하며 계산을 수행함
- 후위 순회가 안성맞춤임을 알 수 있음
수식 트리 구축 방법
- 후위 표기식을 입력 받는다는 가정하에 수식 트리 구축을 살펴보자
- 다음과 같은 과정으로 동작하는 알고리즘 사용
- 수식을 뒤에서 앞쪽으로 읽어나가며 토큰을 취함
- 수식에서 제일 마지막에 있는 토큰으로 뿌리 노드를 생성한다. 후위 표기식에서 가장 마지막에 있는 토큰은 항상 연산자임
- 읽어낸 토큰이 연산자인 경우 가지 노드를 생성하며, 이 토큰 다음에 따라오는 2개의 토큰으로 각각 오른쪽 자식 노드와 왼쪽 자식 노드를 생성한다. 단, 다음 토큰도 연산자인 경우 이 토큰에서 만들어진 하위 트리가 완성된 이후에 읽어낸 토큰으로 왼쪽 자식 노드를 생성한다.
- 읽어낸 토큰이 숫자인 경우 잎 노드를 생성한다
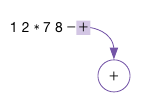



- ex) 12*78-+
- 가장 마지막 토큰 : + --> 뿌리 노드 생성
- '+' 연산자 다음 토큰은 '-' 연산자임
- 또 다른 2개의 토큰이 필요함을 인지
- '-' 토큰으로 뿌리 노드이ㅡ 오른쪽 자식 노드를 만듬
- 또 다른 2개의 토큰이 필요함을 인지
- '-' 노드는 연산자 노드임 --> 양쪽 자식으로 피연산자 필요
- 다음 토큰은 숫자 '8' 이니 오른쪽 자식으로 만들어 넣음
- 그 다음 토큰은 숫자 '7' 이니 왼쪽 자식으로 만들어 넣음
- 새로운 자식 노드들은 모두 숫자를 갖고 있으므로 잎 노드가 됨
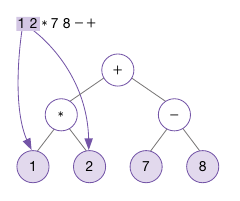
- 다음 토큰인 '*'을 '+' 노드의 왼쪽 자식 노드로 만들어 넣음
- '*' 노드는 연산자 --> 자식 노드들이 필요
- 토큰을 읽어 '2'와 '1'을 얻고 각각 오른쪽 자식 노드와 왼쪽 자식 노드로 만들어 '*'에 붙여 넣음
- 전체 수식 트리 완성
- '+' 연산자 다음 토큰은 '-' 연산자임
- 가장 마지막 토큰 : + --> 뿌리 노드 생성
수식 트리의 구현
- 대부분 함수를 기존 이진 트리에서 그대로 사용
수식 트리 구축
- 입력된 후위 표기식으로부터 수식 트리를 만드는 함수
- 먼저 매개 변수로 입력된 후위 표기식을 뒤부터 읽어 토큰 하나를 분리함
- 읽어낸 토큰이 연산자 --> 2개의 피연산자가 뒤따라온다는 사실을 의미
- 이 경우 방금 읽어낸 연산자 토큰을 노드에 연결하고, 함수를 두 번 호출하여 뒤따라오는 피연산자 둘을 연산자 노드의 양쪽 자식으로 연결
- 처음 읽은 토큰이 피연산자인 경우 해당 토큰을 노드에 입력하고 함수를 반환
void ET_BuildExpressionTree( char* PostfixExpression, ETNode** Node ) {
int len = strlen( PostfixExpression );
char Token = PostfixExpression[ len -1 ];
PostfixExpression[ len-1 ] = '\0';
switch ( Token )
{
// 연산자인 경우
case '+': case '-': case '*': case '/':
(*Node) = ET_CreateNode( Token );
ET_BuildExpressionTree( PostfixExpression, &(*Node)->Right );
ET_BuildExpressionTree( PostfixExpression, &(*Node)->Left );
break;
// 피연산자인 경우
default :
(*Node) = ET_CreateNode( Token);
break;
}
}수식 트리 계산
- 구축된 수식 트리를 이용해 계산을 수행하는 함수
- 노드에 담긴 토큰을 연산자인 경우와 피연산자인 경우로 처리
- 토큰이 연산지일 때는 트리의 바닥(잎) 부터 계산 결과를 병합하여 올라가도록 노드의 양쪽 자식에 대하여 함수 재귀를 호출
- 재귀 호출한 함수가 값을 반환하면 왼쪽 수식 트리의 계산 결과는 Left 변수에, 오른쪽 수식 트리의 결과는 Right 변수에 저장됨
- 그 다음 연산자의 종류에 따라 덧셈, 뺄셈, 곱셈, 나눗셈을 수행
- 토큰이 피연산자인 경우 토큰에 담겨 있던 값을 수로 변환해서 반환
- 토큰이 연산지일 때는 트리의 바닥(잎) 부터 계산 결과를 병합하여 올라가도록 노드의 양쪽 자식에 대하여 함수 재귀를 호출
double ET_Evaluate( ETNode* Tree ) {
char Temp[2];
double Left = 0;
double Right = 0;
double Result = 0;
if ( Tree == NULL )
return 0;
switch ( Tree->Data )
{
// 연산자인 경우
case '+': case '-': case '*': case '/':
Left = ET_Evaluate( Tree->Left );
Right = ET_Evaluate( Tree->Right );
if ( Tree->Data == '+' ) Result = Left + Right;
else if ( Tree->Data == '-' ) Result = Left - Right;
else if ( Tree->Data == '*' ) Result = Left * Right;
else if ( Tree->Data == '/' ) Result = Left / Right;
break;
// 피연산자인 경우
default :
memset(Temp, 0, sizeof(Temp));
Temp[0] = Tree->Data;
Result = atof(Temp);
break;
}
return Result;
}예제 프로그램
#include "ExpressionTree.h"
int main( void ) {
ETNode* Root = NULL;
char PostfixExpression[20] = "71*52-/";
ET_BuildExpressionTree( PostfixExpression, &Root);
// 트리 출력
printf("Preorder ...\n");
ET_PreorderPrintTree( Root );
printf("\n\n");
printf("Inorder ... \n");
ET_InorderPrintTree( Root );
printf("\n\n");
printf("Postorder ... \n");
ET_PostorderPrintTree( Root );
printf("\n");
printf("Evaulation Result : %f \n", ET_Evaluate( Root ) );
// 트리 소멸시키기
ET_DestroyTree( Root );
return 0;
}참조) 박상현, 『이것이 자료구조+알고리즘이다 with C언어』, 한빛미디어(2022)
'Data Structure > 자료구조' 카테고리의 다른 글
| [자료구조] 비선형 문제 (0) | 2024.06.18 |
|---|---|
| [자료구조] 트리 - 분리 집합 (0) | 2024.06.15 |
| [자료구조] 이진 트리 (0) | 2024.06.15 |
| [자료구조] 트리 ADT (0) | 2024.06.15 |
| [자료구조] 덱(Dequeue, 데크) (0) | 2024.03.27 |