힙(heap)
- std::priority_queue에서 다룬 heap에 대해 더 깊이 있게 알아보자
- 힙은 앞서 말했던 것처럼 다음과 같은 시간 복잡도를 만족해야 한다
- O(1) : 최대 원소에 즉각적으로 접근할 수 있어야 한다.
- O(log N) : 원소 삽입에 대한 시간 복잡도
- O(log N) : 최대 원소 삭제에 대한 시간 복잡도
- 원소 삽입 또는 삭제에 대해 O(log N)의 시간 복잡도를 만족하기 위해 트리 구조를 사용해야 한다.
- 특히 이 경우 완전 이진 트리를 사용해야 한다.
- 완전 이진 트리는 트리의 데이터를 배열을 이용하여 저장할 수 있다.
- 루트 노드를 배열 또는 벡터의 맨 처음에 저장하고, 그다음 레벨의 모든 노드는 왼쪽부터 오른쪽 순서로 저장한다
- 포인터를 사용하지 않아서 메모리 사용 측면에서 효율적이다.
- 부모 노드로부터 자식노드로 이동하는 것은 단순히 배열의 인덱스 계산으로 가능하다.
- 부모 노드가 i번째 배열 원소로 저장되어있다면, 자식 노드는 2i + 1 또는 2i +2번째 인덱스로 접근하면 된다
- 자식 노드가 i번째 인덱스라면, 부모 노드는 (i - 1)/2 번째 인덱스이다.
힙의 불변성
- 원소를 삽입하거나 삭제할 때 유지해야 할 조건
- 최대 원소에 즉각적으로 접근 가능해야 한다.
- 이를 위해 최대 원소가 항상 고정된 위치에 있어야 한다
- 힙을 구현할 때는 최대 원소가 트리의 루트에 있도록 설정한다
- 이를 위해 부모 노드가 두 자식 노드보다 항상 커야 한다는 불변성을 유지하도록 설정해야 한다.
- 이렇게 구성한 힙을 최대 힙(max heap) 이라고 한다.
- 반대로 최소 원소에 빠르게 접근할 수 있도록 힙을 구성할 수 있다
- 모든 비교 연산을 반대로 설정하면 된다
- 이렇게 만들어진 힙을 최소 힙(min heap) 이라고 한다.
- 최대 원소에 즉각적으로 접근 가능해야 한다.
힙 연산
원소 삽입
힙의 불변성을 고려하면서 살펴보자
먼저, 완전 이진 트리를 유지해야 한다.
- 새 원소를 삽입하려면 단순히 배열의 맨 마지막 위치에 원소를 추가하면 된다
- 마지막 레벨이 꽉 차있다면 새로운 레벨을 추가하여 노드를 추가한다
그리고, 모든 노드는 자식 노드보다 더 큰 값을 가지고 있어야 한다
- 새로운 원소를 트리의 맨 마지막 위치에 추가한 후에는 이 조건이 성립되지 않을 가능성이 생긴다
- 이를 해결하기 위해 새로 삽입한 원소의 부모 노드와 값을 비교하고, 만약 부모 노드가 더 작으면 서로 교환한다.
- 여전히 새 원소가 새 부모 노드보다 큰 값을 가질 수 있으므로, 교환 작업을 반복해야 한다.

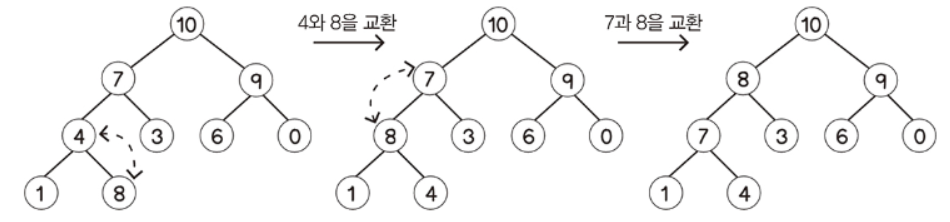
- 완전 이진 트리의 높이는 최대 log N이므로, 시간 복잡도는 O(log N)으로 표현할 수 있다.
원소 삭제
- 힙에서는 가장 큰 원소만 삭제할 수 있다.(최대 힙 기준)
- 다른 원소에는 직접 접근할 수 없기 때문
- 최대 원소는 항상 루트에 존재하므로, 루트 노드를 삭제해야 한다.
- 루트를 삭제할 경우, 어느 노드를 이용하여 루트를 대체할 것인지 결정해야 한다.
이를 위해
- 루트 노드와 트리의 맨 마지막 노드를 서로 교환한다.
- 마지막 노드를 삭제한다
- 다만 최대 원소는 삭제했지만, 루트 위치에서 부모 노드가 자식 노드보다 커야 한다는 불변성을 만족하지 못하게 된다
이를 위해
- 루트 노드와 두 자식 노드를 서로 비교하여 그 중 더 큰 노드와 교환한다.
- 서브 트리에 대해서도 노드 교환 작업을 재귀적으로 반복한다

- 교환 작업의 최대 횟수는 트리의 높이와 같으므로, 원소 삭제의 시간 복잡도는 O(lon N)으로 표현할 수 있다
힙 초기화
- 벡터, 리스트, 덱과는 달리 힙은 불변성을 유지해야 하기 때문에 초기화가 간단하지 않다.
- 힙에 하나씩 원소를 삽입하는 방법이 가장 간단하나, O(Nlog N)의 시간 복잡도를 가지며 효율적이지 않다.
- 힙 생성 알고리즘(heapification algorithm)을 사용하면 O(N) 시간에 힙을 초기화할 수 있다.
- 전체 트리의 아래쪽 서브 트리부터 힙 불변 속성을 만족하도록 힙을 업데이트 하는 방식이다
- 맨 마지막 레벨부터, 한 레벨씩 트리 위로 올라가면서 힙 속성을 만족하도록 트리를 업데이트한다.
- 이 작업은 O(N)의 시간 복잡도를 갖는다
- 다행히 C++ 표준은 배열 또는 벡터의 반복자를 인자로 받아 힙을 구성하는 std::make_heap() 함수를 제공한다
Example) 중앙값 구하기
- 가장 간단한 방법은 매번 데이터를 받을 때 마다 모든 데이터를 정렬하고, 가운데 원소를 반환하는 것이다.
- 이러한 작업은 정렬 연산 때문에 O(Nlog N)의 시간복잡도를 갖는다
- 힙을 이용하여 최적화하는 방법을 알아보자
- 최대 힙, 최소 힙 2개를 이용하여 새로 들어온 데이터가 기존 데이터의 중앙값보다 작으면 최대 힙에 저장하고, 크면 최소 힙에 저장한다
- 두 힙의 최상단 원소를 이용하여 중앙값을 계산할 수 있게 된다
#include <iostream>
#include <queue>
#include <vector>
struct median
{
std::priority_queue<int> maxHeap;
std::priority_queue<int, std::vector<int>, std::greater<int>> minHeap;
void insert(int data)
{
if(maxHeap.size() == 0)
{
maxHeap.push(data);
return;
}
if(maxHeap.size() == minHeap.size())
{
if(data <= get())
maxHeap.push(data);
else
minHeap.push(data);
return;
}
if(maxHeap.size() < minHeap.size())
{
if(data > get())
{
maxHeap.push(minHeap.top());
minHeap.pop();
minHeap.push(data);
}
else
maxHeap.push(data);
return;
}
if(data < get())
{
minHeap.push(maxHeap.top());
maxHeap.pop();
maxHeap.push(data);
}
else
minHeap.push(data);
}
double get()
{
if(maxHeap.size() == minHeap.size())
return (maxHeap.top() + minHeap.top()) / 2.0;
if(maxHeap.size() < minHeap.size())
return minHeap.top();
return maxHeap.top();
}
};
int main()
{
median med;
med.insert(1);
std::cout << "1 삽입 후 중앙 값 : " << med.get() << std::endl;
med.insert(5);
std::cout << "5 삽입 후 중앙 값 : " << med.get() << std::endl;
med.insert(2);
std::cout << "2 삽입 후 중앙 값 : " << med.get() << std::endl;
med.insert(10);
std::cout << "10 삽입 후 중앙 값 : " << med.get() << std::endl;
med.insert(40);
std::cout << "40 삽입 후 중앙 값 : " << med.get() << std::endl;
return 0;
}'Programming Language(Sub) > C++' 카테고리의 다른 글
| [C++ STL] 3.4 C++ 해시 테이블 (0) | 2024.06.23 |
|---|---|
| [C++ STL] 2.6 그래프(graph) (0) | 2024.06.21 |
| [C++ STL] 1.8 컨테이너 어댑터(Container Adaptor) (0) | 2024.06.15 |
| [C++ STL] 1.7 std::dequeue (0) | 2024.06.15 |
| [C++ STL] 1.6 std::list (0) | 2024.06.15 |